2017年辽宁省营口市中考数学一模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题

1. 2017的相反数是（）

A、2017 B、﹣2017 C、 $\frac{1}{2017}$ D、﹣ $\frac{1}{2017}$

查看试题解析
2. 下列计算正确的是（）

A、3a+4b=7ab B、（ab³）²=ab⁶ C、（a+2）²=a²+4 D、x¹²÷x⁶=x⁶

查看试题解析
3. 如图是一个由4个相同的正方体组成的立体图形，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量，如表所示：
用电量（度）
120
140
160
180
200
户数
2
3
6
7
2
则这20户家庭该月用电量的众数和中位数分别是（）

A、180，160 B、160，180 C、160，160 D、180，180

查看试题解析
5. 如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，要说明∠D′O′C′=∠DOC，需要证明△D′O′C′≌△DOC，则这两个三角形全等的依据是（）

A、边边边 B、边角边 C、角边角 D、角角边

查看试题解析
7. 小玲每天骑自行车或步行上学，她上学的路程为2800米，骑自行车的平均速度是步行平均速度的4倍，骑自行车比步行上学早到30分钟．设小玲步行的平均速度为x米/分，根据题意，下面列出的方程正确的是（）

A、 $\frac{2800}{x} - \frac{2800}{4 x} = 30$ B、 $\frac{2800}{4 x} - \frac{2800}{x} = 30$ C、 $\frac{2800}{x} - \frac{2800}{5 x} = 30$ D、 $\frac{2800}{5 x} - \frac{2800}{x} = 30$

查看试题解析
8. 不等式2x+3＞3x+2的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（）

A、5 B、4 C、3 D、2

查看试题解析
10. 如图，点A是反比例函数y= $\frac{k}{x}$ 的图象上的一点，过点A作AB⊥x轴，垂足为B．点C为y轴上的一点，连接AC，BC．若△ABC的面积为4，则k的值是（）

A、4 B、﹣4 C、8 D、﹣8

查看试题解析

二、填空题

11. 在函数 $y = \frac{\sqrt{1 - x}}{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 因式分解：﹣2x²y+12xy﹣18y= ．

查看试题解析
13. PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为．

查看试题解析
14. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号是奇数的概率为．

查看试题解析
15. 如图，已知点A、B、C、D均在以BC为直径的圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10，则图中阴影部分的面积为．

查看试题解析
16. 如图，△ABC中，AD⊥BC，垂足为D，AD=BD=3，CD=2，点E从点B出发沿线段BA的方向移动到点A停止，连接CE．若△ADE与△CDE的面积相等，则线段DE的长度是．

查看试题解析
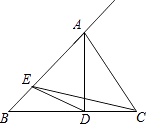17. 如图，在半径为3的⊙O中，直径AB与弦CD相交于点E，连接AC，BD，若AC=2，则cosD= ．

查看试题解析
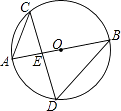18. 函数y=x²+bx+c与y=x的图象如图所示，有以下结论：①b²﹣4c＞0；②b+c+1=0；③3b+c+6=0；④当1＜x＜3时，x²+（b﹣1）x+c＜0；其中正确的个数有个．

查看试题解析

三、解答题

19. 先化简，再求值：（ $\frac{x^{2} - 1}{x^{2} - 2 x + 1}$ ﹣x﹣1）÷ $\frac{x + 1}{x - 1}$ ，其中x=（ $\frac{1}{3}$ ）^﹣¹+ $\sqrt[3]{- 125}$ +4sin30°．

查看试题解析
20. 为了了解青少年形体情况，现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况．我们对测评数据作了适当处理（如果一个学生有一种以上不良姿势，以他最突出的一种作记载），并将统计结果绘制了如下两幅不完整的统计图，请你根据图中所给信息解答下列问题：

(1)、请将两幅统计图补充完整；

(2)、请问这次被抽查形体测评的学生一共是多少人？

(3)、如果全市有5万名初中生，那么全市初中生中，坐姿和站姿不良的学生有多少人？

查看试题解析
21. 如图，转盘上1、2、3、4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票（每种邮票各两枚，鸡年邮票面值“80分”，其它邮票都是面值“1.20元”），转动转盘后，指针每落在某个数字所在扇形一次就表示获得该种邮票一枚．

(1)、任意转动转盘一次，获得猴年邮票的概率是；

(2)、任意转动转盘两次，求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率．

查看试题解析
22.
如图，是某广场台阶（结合轮椅专用坡道）景观设计的模型，以及该设计第一层的截面图，第一层有十级台阶，每级台阶的高为0.15米，宽为0.4米，轮椅专用坡道AB的顶端有一个宽2米的水平面BC；《城市道路与建筑物无障碍设计规范》第17条，新建轮椅专用坡道在不同坡度的情况下，坡道高度应符合以下表中的规定：
坡度
1：20
1：16
1：12
最大高度（米）
1.50
1.00
0.75

(1)、选择哪个坡度建设轮椅专用坡道AB是符合要求的？说明理由；

(2)、求斜坡底部点A与台阶底部点D的水平距离AD．

查看试题解析
23. 如图，以△ABC的BC边上一点O为圆心，经过A，C两点且与BC边交于点E，点D为CE的下半圆弧的中点，连接AD交线段EO于点F，若AB=BF．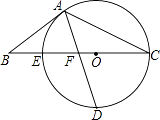

(1)、求证：AB是⊙O的切线；

(2)、若CF=4，DF= $\sqrt{10}$ ，求⊙O的半径r及sinB．

查看试题解析
24. 某企业接到一批粽子生产任务，按要求在15天内完成，约定这批粽子的出厂价为每只6元，为按时完成任务，该企业招收了新工人，设新工人李明第x天生产的粽子数量为y只，y与x满足下列关系式：
y= ${\begin{matrix} 54 x & (0 \leq x \leq 5) \\ 30 x + 120 & (5 < x \leq 15) \end{matrix}$ ．

(1)、李明第几天生产的粽子数量为420只？

(2)、如图，设第x天每只粽子的成本是p元，p与x之间的关系可用图中的函数图象来刻画．若李明第x天创造的利润为w元，求w与x之间的函数表达式，并求出第几天的利润最大，最大利润是多少元？（利润=出厂价﹣成本）

(3)、设（2）小题中第m天利润达到最大值，若要使第（m+1）天的利润比第m天的利润至少多48元，则第（m+1）天每只粽子至少应提价几元？

查看试题解析
25.
爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．

(1)、如图1，当tan∠PAB=1，c=4 $\sqrt{2}$ 时，a= ， b=；
如图2，当∠PAB=30°，c=2时，a= ， b=；

(2)、请你观察（1）中的计算结果，猜想a²、b²、c²三者之间的关系，用等式表示出来，并利用图3证明你的结论．

(3)、如图4，▱ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 $\sqrt{5}$ ，AB=3，求AF的长．

查看试题解析
26.
已知抛物线y=ax²+bx+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x²﹣10x+16=0的两个根，且抛物线的对称轴是直线x=﹣2．

(1)、求A、B、C三点的坐标；

(2)、求此抛物线的表达式；

(3)、连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

(4)、在（3）的基础上试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

查看试题解析

用电量（度）	120	140	160	180	200
户数	2	3	6	7	2

坡度	1：20	1：16	1：12
最大高度（米）	1.50	1.00	0.75