2017年江苏省泰州市泰兴市中考数学一模试卷
试卷更新日期：2017-07-20 类型：中考模拟
一、选择题
-
1. 2017的倒数是（ ）A、 B、﹣ C、2017 D、﹣20172. 从国家旅游局获悉，2017年春节期间，全国共接待游客3.44亿人次，实现旅游总收入423300000000元．将423300000000元用科学记数法表示为（ ）A、4.233×103元 B、0.4233×104元 C、42.33×1010元 D、4.233×1011元3. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
4. 某几何体的主视图和左视图如图所示，则该几何体可能是（ ）
A、长方体 B、圆锥 C、圆柱 D、球5.若干名同学制作卡通图片，他们制作的卡通图片张数的条形统计图如图所示，设他们制作的卡通图片的张数的平均数为a，中位数为b，众数为c，则a，b，c的大小关系为（ ）
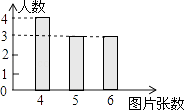A、a＞b＞c B、b＞a＞c C、b＞c＞a D、c＞a＞b6. 如图，半径为1的半圆的圆心在原点，直径AB在x轴上，过原点的任意一条半径与半圆交于点P，过P作PN垂直于x轴，N为垂足，则∠OPN的平分线过定点（ ）
A、（0，﹣1） B、（0，﹣ ） C、（0，﹣ ） D、（0，﹣ ）二、填空题
-
7. ﹣8的立方根是 ．8. 如图放置的一个正五边形ABCDE和正方形ABFG边长相等，则∠1=度．
9. 不等式组 的解集是 ．10. 如图，是某射手在相同条件下进行射击训练的结果统计图，该射手击中靶心的概率的估计值为 ．
11. 如图，直线m∥n，△ABC的顶点B，C分别在直线n，m上，且∠ACB=90°，若∠1=40°，则∠2等于度．
12. 二次函数y=x2﹣2x+3的图象向左平移一个单位，再向上平移两个单位后，所得二次函数的解析式为 ．13. 如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是 ．
14. 关于x的一元二次方程x2+（2m+1）x+m2﹣1=0有两个不相等的实数根，则m的取值范围是 ．15. 如图，△ABC的三个顶点都在正方形网格的格点上，则sin∠ACB的值为 ．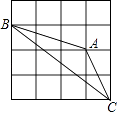
16. 如图，正方形ABCD和正方形CGEF的边长分别是3和5，且点B、C、G在同一直线上，M是线段AE的中点，连接MF，则MF的长为 ．
三、解答题
-
17. 综合题。(1)、计算：（﹣ ）﹣2+2cos30°﹣|﹣ |﹣（π﹣2017）0(2)、化简：（ ﹣x+1）÷ ．18. 某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过调查获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：
(1)、这次活动一共调查了名学生；(2)、补全条形统计图，并求出扇形统计图中选择篮球项目的人数所在扇形的圆心角的度数；(3)、若该学校有1200人，则该学校选择足球项目的学生人数约是多少？19. 如图，转盘A、B中各个扇形的面积相等，且分别标有数字．小明和小丽玩转转盘游戏，规则如下：分别转动转盘A、B，当转盘停止转动时，将两个指针所指扇形内的数字相乘（若指针停在等分线上，那么重转一次）．
(1)、用列表法（或树状图）分别求出数字之积为3的倍数及数字之积为5的倍数的概率；(2)、小亮和小丽想用这两个转盘做游戏，他们规定：数字之积为3的倍数时，小亮得3分；数字之积为5的倍数时，小丽得4分，这个游戏对双方公平吗？请说明理由；认为不公平的，请你修改得分规定，使游戏双方公平．20. 为响应“足球进校园”的号召，某学校决定在商场购买甲、乙两种品牌的足球．已知乙种品牌足球比甲种品牌足球每只贵10元，该校欲分别花费2000元、1200元购买甲、乙两种足球，这样购得甲种足球的数量是购得乙种足球的数量的2倍．求甲、乙两种足球的单价．21. 如图，在△ABC中，∠C=90°，点D为边BC上一点，点E为边AB的中点，过点A作AF∥BC，交DE的延长线与点F，连接BF．
(1)、求证：四边形ADBF是平行四边形；(2)、若∠ADF=∠BDF，DF=2CD，求∠ABC的度数．22.如图，一艘轮船在A处时观测得小岛C在船的北偏东60°方向，轮船以40海里/时的速度向正东方向航行1.5小时到达B处，这时小岛C在船的北偏东30°方向．已知小岛C周围50海里范围内是暗礁区．
(1)、求B处到小岛C的距离(2)、若轮船从B处继续向东方向航行，有无触礁危险？请说明理由．（参考数据： ≈1.73）
23. 如图，已知AB是⊙O的直径，C是⊙O上的点，且OE⊥AC于点E，过点C作⊙O的切线，交OE的延长线于点D，交AB的延长线于点F，连接AD
(1)、求证：AD是⊙O的切线；(2)、若tan∠F= ，⊙O半径为1，求线段AD的长．24. 如图，反比例函数y1= 的图象与一次函数y2= x的图象交于点A、B，点B的横坐标是4，点P（1，m）在反比例函数y1= 的图象上．
(1)、求反比例函数的表达式；(2)、观察图象回答：当x为何范围时，y1＞y2；(3)、求△PAB的面积．25.如图，矩形ABCD中，AB=3，BC=4，点E是线段CB上的异于B、C的动点，AF⊥AE交线段CD的延长线于点F，EF与AD交于点M．
(1)、求证：△ABE∽△ADF；(2)、若AE⊥BD，求BE长；(3)、若△AEM是以AE为腰的等腰三角形，求BE的长．26.如图，抛物线y=ax2﹣（a+1）x﹣3与x轴交于点A、B，与y轴交于点C，∠BCO=45°，点M为线段BC上异于B、C的一动点，过点M与y轴平行的直线交抛物线于点Q，点R为线段QM上一动点，RP⊥QM交直线BC于点P．设点M的横坐标为m．
(1)、求抛物线的表达式；(2)、当m=2时，△PQR为等腰直角三角形，求点P的坐标；(3)、①求PR+QR的最大值；②求△PQR面积的最大值．