2017年江苏省泰州市靖江市中考数学一模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列四个数中，最大的数是（）

A、﹣2 B、2π C、0 D、6

查看试题解析
2. 据报道，目前我国“天河二号”超级计算机的运算速度位居全球第一，其运算速度达到了每秒338 600 000亿次，数字338 600 000用科学记数法可简洁表示为（）

A、3.386×10⁸ B、0.3386×10⁹ C、33.86×10⁷ D、3.386×10⁹

查看试题解析
3. 若一个三角形三个内角度数的比为1：2：3，那么这个三角形最小角的正切值为（　　）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
4. 如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AD=1，DB=2，则△ADE的面积与△ABC的面积的比等于（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{8}$ D、 $\frac{1}{9}$

查看试题解析
5. 如图，在5×5的正方形网格中，从在格点上的点A，B，C，D中任取三点，所构成的三角形恰好是直角三角形的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
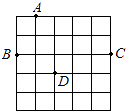6. 已知直线y=﹣ $\sqrt{3}$ x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣ $\frac{1}{3}$ （x﹣ $\sqrt{3}$ ）²+4上，能使△ABP为等腰三角形的点P的个数有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

7. 函数 $y = \sqrt{x - 2}$ 中自变量x的取值范围是．

查看试题解析
8. 分解因式：ax²﹣ay²= ．

查看试题解析
9. 某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆，则该几何体是．

查看试题解析
10. 已知正n边形的一个内角为135°，则边数n的值是．

查看试题解析
11. 两块大小一样斜边为4且含有30°角的三角板如图水平放置．将△CDE绕C点按逆时针方向旋转，当E点恰好落在AB上时，△CDE旋转了度，线段CE旋转过程中扫过的面积为．

查看试题解析
12. 如图，△ABC内接于⊙O，AC是⊙O的直径，∠ACB=50°，点D是 $\hat{B A C}$ 上一点，则∠D=度．

查看试题解析
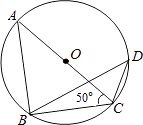13. 如图，在矩形ABCD中，对角线AC、BD相交于点O，若AE平分∠BAD交BC于点E，且BO=BE，连接OE，则∠BOE= ．

查看试题解析
14. 如图，在平面直角坐标系中，二次函数y=﹣3x²的图象经过平移得到二次函数y=﹣3x²+6x﹣6的图象，则二次函数y=﹣3x²图象的对称轴与两段抛物线所围成的阴影部分的面积为．

查看试题解析
15. 一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后分别按原速同时驶往甲地，两车之间的距离S（km）与慢车行驶时间t（h）之间的函数图象如图所示，则快车到达甲地时，慢车距离甲地 km．

查看试题解析
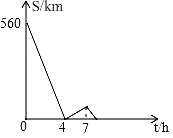16. 如图，AB是半圆O的直径，点C在半圆O上，AB=4cm，∠CAB=60°，P是弧 $\hat{B C}$ 上的一个动点，连接AP，过C点作CD⊥AP于D，连接BD，在点P移动的过程中，BD的最小值是．

查看试题解析

三、解答题

17. 计算或化简：

(1)、计算：2^﹣¹+ $\sqrt{3}$ cos30°+|﹣5|﹣（π﹣2017）⁰

(2)、化简：（x﹣5+ $\frac{16}{x + 3}$ ）÷ $\frac{x - 1}{x^{2} - 9}$ ．

查看试题解析
18. 甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．

(1)、请用列表法或画树状图的方法，求两人抽取相同数字的概率；

(2)、若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．

查看试题解析
19. 为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息，解答下列问题：

(1)、a= ， b= ，且补全频数分布直方图；

(2)、若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？

(3)、若我市初中生共有16000人，竞赛活动获奖率为40%，获三等奖以上的学生表示对“足球比较喜欢”，请你估计我市初中生对“足球比较喜欢”的有多少人？

查看试题解析
20. 如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：

(1)、△AEH≌△CGF；

(2)、四边形EFGH是菱形．

查看试题解析
21. 政府为开发“江心岛O”，从仓储D处调集物资，计划先用汽车运到与D在同一直线上的C，B，A三个码头中的一处，再用货船运到小岛O．已知：OA⊥AD，∠ODA=15°，∠OCA=30°，∠OBA=45°，CD=20km．若汽车行驶的速度为50km/时，货船航行的速度为25km/时，

(1)、求B、C两个码头之间的距离；

(2)、这批物资在哪个码头装船，最早运抵小岛O？（在物资搬运能力上每个码头工作效率相同，参考数据： $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7）．

查看试题解析
22. 如图，AB是半圆O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC

(1)、求证：BC平分∠PBD；

(2)、求证：PC²=PA•PB；

(3)、若PA=2，PC=2 $\sqrt{3}$ ，求阴影部分的面积（结果保留π）

查看试题解析
23. 骑自相车旅行越来越受到人们的喜爱，顺风车行经营的A型车2016年4月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售比去年增加400元，若今年4月份与去年4月份卖出的A型车数量相同，则今年4月份A型车销售总额将比去年4月份销售总额增加25%．
A、B两种型号车的进货和销售价格如表：
A型车
B型车
进货价格（元/辆）
1100
1400
销售价格（元/辆）
今年的销售价格
2400

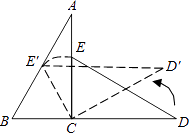
(1)、求今年4月份A型车每辆销售价多少元（用列方程的方法解答）；

(2)、该车行计划5月份新进一批A型车和B型车共50辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？

查看试题解析
24. 已知反比例函数y= $\frac{k}{x}$ 的图象经过点A（﹣ $\sqrt{3}$ ，1）．

(1)、试确定此反比例函数的解析式；

(2)、点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB．判断点B是否在此反比例函数的图象上，并说明理由；

(3)、已知点P（m， $\sqrt{3}$ m+6）也在此反比例函数的图象上（其中m＜0），过P点作x轴的垂线，交x轴于点M．若线段PM上存在一点Q，使得△OQM的面积是 $\frac{1}{2}$ ，设Q点的纵坐标为n，求n²﹣2 $\sqrt{3}$ n+9的值．

查看试题解析
25. 综合题。

(1)、
如图1，在正方形ABCD中，点E，H分别在BC，AB上，AE与DH交于O，若AE=DH，求证：AE⊥DH；

(2)、
如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，EF与GH交于O，若EF=HG，探究线段EF与HG的位置关系，并说明理由；

(3)、
如图3所示，在（2）问条件下，若HF∥GE，试探究线段FH、线段EG与线段EF的数量关系，并说明．

查看试题解析
26. 在平面直角坐标系xOy中，抛物线y=﹣x²+bx+c与x轴交于点A，B（A在B的左侧），抛物线的对称轴为直线x=1，AB=4．

(1)、求抛物线的表达式；

(2)、抛物线上有两点M（x₁ ， y₁）和N（x₂ ， y₂），若x₁＜1，x₂＞1，x₁+x₂＞2，试判断y₁与y₂的大小，并说明理由；

(3)、直线l过A及C（0，﹣2），P为抛物线上一点（在x轴上方），过P作PD∥y轴交直线AC于点D，以PD为直径作⊙E，求⊙E在直线AC上截得的线段的最大长度．

查看试题解析

获奖等次	频数	频率
一等奖	10	0.05
二等奖	20	0.10
三等奖	30	b
优胜奖	a	0.30
鼓励奖	80	0.40

	A型车	B型车
进货价格（元/辆）	1100	1400
销售价格（元/辆）	今年的销售价格	2400