2017年吉林省长春市农安县中考数学模拟试卷(4月份)
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣3的相反数是( )A、﹣ B、 C、﹣3 D、32. 2017年春节期间(1月27日至2月2日),长春龙嘉国际机场保障航班起降1695架次,运送旅客大约228600人次,228600这个数用科学记数法表示为( )A、22.86×104 B、2.286×105 C、2.286×106 D、0.2286×1063. 如图是由5个相同的小正方体组成的立体图形,这个立体图形的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 不等式组 的解集在数轴上表示正确的是( )A、
4. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 方程x2+4x+4=0的根的情况是( )A、有两个相等的实数根 B、只有一个实数根 C、没有实数根 D、有两个不相等的实数根6. 如图是棋盘的一部分,若用(1,3)表示
5. 方程x2+4x+4=0的根的情况是( )A、有两个相等的实数根 B、只有一个实数根 C、没有实数根 D、有两个不相等的实数根6. 如图是棋盘的一部分,若用(1,3)表示 的位置,(2,2)表示
的位置,(2,2)表示  的位置,则
的位置,则  的位置可表示为( )
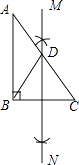
的位置可表示为( )  A、(1,6) B、(6,1) C、(6,0) D、(7,2)7. 如图,⊙O是△ABC的外接圆,点C、O在弦AB的同侧.若∠ACB=40°,则∠ABO的大小为( )
A、(1,6) B、(6,1) C、(6,0) D、(7,2)7. 如图,⊙O是△ABC的外接圆,点C、O在弦AB的同侧.若∠ACB=40°,则∠ABO的大小为( ) A、40° B、45° C、50° D、60°8. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( )
A、40° B、45° C、50° D、60°8. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( ) A、2 B、4 C、2 D、4
A、2 B、4 C、2 D、4二、填空题
-
9. 计算:(a3)2= .10. 分解因式:2x2﹣18= .11. 如图,在Rt△ABC中,∠C=90°.以点A为圆心、AC长为半径作圆弧,交边AB于点D.若∠B=65°,AC=6,则 的长为 .
 12. 如图,在Rt△ABC中,∠B=90°,按如下步骤作图:
12. 如图,在Rt△ABC中,∠B=90°,按如下步骤作图:①分别以点B、C为圆心,大于 AB的长为半径作弧,两弧相交于点M和N;
②作直线MN交AC于点D,
③连接BD,
若AC=8,则BD的长为 .
 13. 如图,在平面直角坐标系中,点P(﹣ ,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是 .
13. 如图,在平面直角坐标系中,点P(﹣ ,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是 .
14. 如图,在平面直角坐标系中,正方形ABCD的三个顶点A、B、D均在抛物线y=ax2﹣4ax+3(a<0)上.若点A是抛物线的顶点,点B是抛物线与y轴的交点,则AC长为 .
三、解答题
-
15. 先化简,再求值:a(a+1)﹣(a﹣1)2 , 其中a= .16. 三张扑克牌的牌面如图所示,这三张扑克牌除牌面不同外,其它均相同.将这三张扑克牌背面朝上洗匀,从中随机抽出一张,记下数字后放回;重新洗匀后从中再随机抽出一张,记下数字.请用画树状图(或列表)的方法,求抽出的两张扑克牌上的数字之和是9的概率.
 17. 为了减少雾霾,美化环境,小王上班的交通方式由驾车改为骑自行车,小王家距单位的路程是15千米,在相同的路线上,小王驾车的速度是骑自行车速度的4倍,小王每天骑自行车上班比驾车上班要早出发45分钟,才能按原时间到达单位,求小王骑自行车的速度.18.
17. 为了减少雾霾,美化环境,小王上班的交通方式由驾车改为骑自行车,小王家距单位的路程是15千米,在相同的路线上,小王驾车的速度是骑自行车速度的4倍,小王每天骑自行车上班比驾车上班要早出发45分钟,才能按原时间到达单位,求小王骑自行车的速度.18.如图,在热气球上A处测得塔顶B的仰角为52°,测得塔底C的俯角为45°,已知A处距地面98米,求塔高BC.(结果精确到0.1米)
【参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28】
 19. 为了解某小区家庭用水情况,小丽随机调查了该小区部分家庭4月份的用水量,并将收集的数据整理并绘制成如下条形统计图.
19. 为了解某小区家庭用水情况,小丽随机调查了该小区部分家庭4月份的用水量,并将收集的数据整理并绘制成如下条形统计图. (1)、求小丽调查的家庭总数?(2)、所调查家庭4月份用水量的众数为吨,中位数为吨.(3)、该小区共有200户家庭,请估计这个小区4月份的用水总量.20. 如图(1),在△ABC中,AD是BC边的中线,过A点作AE∥BC与过D点作DE∥AB交于点E,连接CE.
(1)、求小丽调查的家庭总数?(2)、所调查家庭4月份用水量的众数为吨,中位数为吨.(3)、该小区共有200户家庭,请估计这个小区4月份的用水总量.20. 如图(1),在△ABC中,AD是BC边的中线,过A点作AE∥BC与过D点作DE∥AB交于点E,连接CE. (1)、求证:四边形ADCE是平行四边形.(2)、连接BE,AC分别与BE、DE交于点F、G,如图(2),若AC=6,求FG的长.
(1)、求证:四边形ADCE是平行四边形.(2)、连接BE,AC分别与BE、DE交于点F、G,如图(2),若AC=6,求FG的长. 21. 某县在实施“村村通”工程中,决定在A、B两村之间修一条公路,甲、乙两个工程队分别从A、B两村同时开始相向修路,施工期间,甲队改变了一次修路速度,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到公路修通,甲、乙两个工程队各自所修公路的长度y(米)与修路时间x(天)之间的函数图象如图所示.
21. 某县在实施“村村通”工程中,决定在A、B两村之间修一条公路,甲、乙两个工程队分别从A、B两村同时开始相向修路,施工期间,甲队改变了一次修路速度,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到公路修通,甲、乙两个工程队各自所修公路的长度y(米)与修路时间x(天)之间的函数图象如图所示. (1)、求甲队前8天所修公路的长度;(2)、求甲工程队改变修路速度后y与x之间的函数关系式;(3)、求这条公路的总长度.22. 问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE,
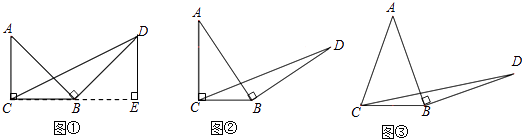
(1)、求甲队前8天所修公路的长度;(2)、求甲工程队改变修路速度后y与x之间的函数关系式;(3)、求这条公路的总长度.22. 问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE,易证△ABC≌△BDE,从而得到△BCD的面积为 .
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
 23. 如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).
23. 如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3). (1)、当点N落在边BC上时,求t的值.(2)、当点N到点A、B的距离相等时,求t的值.(3)、当点Q沿D→B运动时,求S与t之间的函数表达式.(4)、设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF与四边形PQMN的面积比为2:3时t的值.24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m.
(1)、当点N落在边BC上时,求t的值.(2)、当点N到点A、B的距离相等时,求t的值.(3)、当点Q沿D→B运动时,求S与t之间的函数表达式.(4)、设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF与四边形PQMN的面积比为2:3时t的值.24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m. (1)、求这条抛物线所对应的函数表达式.(2)、求这条抛物线的对称轴将矩形QPEF的面积分为1:2两部分时m的值.(3)、求d与m之间的函数关系式及d随m的增大而减小时d的取值范围.(4)、当矩形QPEF的对角线互相垂直时,直接写出其对称中心的横坐标.
(1)、求这条抛物线所对应的函数表达式.(2)、求这条抛物线的对称轴将矩形QPEF的面积分为1:2两部分时m的值.(3)、求d与m之间的函数关系式及d随m的增大而减小时d的取值范围.(4)、当矩形QPEF的对角线互相垂直时,直接写出其对称中心的横坐标.