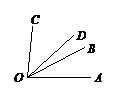初中数学浙教版七年级上册6.7 角的和差 强化提升训练
试卷更新日期:2019-11-27 类型:同步测试
一、单选题
-
1. 如图,OC为 内一条直线,下列条件中不能确定OC平分 的是
 A、 B、 C、 D、2. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
A、 B、 C、 D、2. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) A、240° B、360° C、480° D、540°3. 如图,用一副三角板画角,不可能画出的角的度数是( )
A、240° B、360° C、480° D、540°3. 如图,用一副三角板画角,不可能画出的角的度数是( ) A、120° B、85° C、135° D、165°4. 中午12点15分时,钟表上的时针和分针所成的角是( )A、 B、 C、 D、5. 过∠AOB的顶点作射线OC,下列条件中:①∠AOC=BOC;②∠AOB=2∠AOC;③∠AOB=2∠BOC;④∠AOC+∠BOC=∠AOB.其中能判断射线OC为∠AOB的平分线的个数是( )
A、120° B、85° C、135° D、165°4. 中午12点15分时,钟表上的时针和分针所成的角是( )A、 B、 C、 D、5. 过∠AOB的顶点作射线OC,下列条件中:①∠AOC=BOC;②∠AOB=2∠AOC;③∠AOB=2∠BOC;④∠AOC+∠BOC=∠AOB.其中能判断射线OC为∠AOB的平分线的个数是( )
A、0个 B、1个 C、2个 D、3个6. 如图所示,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD(不包括∠FCD)相等的角有( )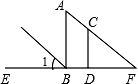 A、5个 B、2个 C、3个 D、4个7. 已知α,β是两个钝角,计算 (α+β)的值,甲,乙,丙,丁四位同学算出了四种不同的答案分别为24°、48°、76°、86°,其中只有一个答案是正确的,则正确的答案是( )A、86° B、76° C、48° D、24°8. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD, ∠AOC=30°时,∠BOD度数为( )A、60° B、120° C、60°或90° D、60°或120°
A、5个 B、2个 C、3个 D、4个7. 已知α,β是两个钝角,计算 (α+β)的值,甲,乙,丙,丁四位同学算出了四种不同的答案分别为24°、48°、76°、86°,其中只有一个答案是正确的,则正确的答案是( )A、86° B、76° C、48° D、24°8. 在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD, ∠AOC=30°时,∠BOD度数为( )A、60° B、120° C、60°或90° D、60°或120°二、填空题
-
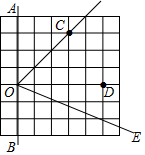
9. 如图,在正方形网格中,点O、A、B、C、D均是格点.若OE平分∠BOC,则∠DOE的度数为°.
 10. 如图, : : :7:4,OM平分 , ,则 的度数为度
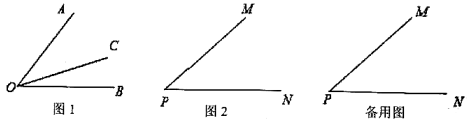
10. 如图, : : :7:4,OM平分 , ,则 的度数为度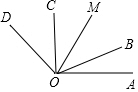 11. 如图,线段OA绕点O逆时针旋转一周,满足∠EOF始终在∠AOB的内部且∠EOF=58°,线段OM、ON分别为∠AOE和∠BOF的平分线,在旋转过程中,∠MON的最大值是 .
11. 如图,线段OA绕点O逆时针旋转一周,满足∠EOF始终在∠AOB的内部且∠EOF=58°,线段OM、ON分别为∠AOE和∠BOF的平分线,在旋转过程中,∠MON的最大值是 . 12. 如图,∠AOB=150°,射线OC与射线OA重合,现在把射线OC绕O点顺时针方向旋转角度α(0°<α<180°),若OD平分∠AOC,且∠AOD与∠BOC互余,则角度α的值为 .
12. 如图,∠AOB=150°,射线OC与射线OA重合,现在把射线OC绕O点顺时针方向旋转角度α(0°<α<180°),若OD平分∠AOC,且∠AOD与∠BOC互余,则角度α的值为 .
13. 已知一条射线OA,在同一平面内从点O再作两条射线OB和OC,使∠AOB=80°,∠BOC=30°,则∠AOC的度数是 .三、解答题
-
14. 如图,射线OA、OC在射线OB的异侧且∠BOC = 2∠AOB (∠AOB<60°),射线OD平分∠AOC,请探求∠BOD与∠AOB的数量关系.