人教新课标A版选修1-1数学1.3简单的逻辑联结词同步检测

试卷更新日期：2016-02-18 类型：同步测试

进入出卷网下载

一、选择题

1. 已知命题 p 所有有理数都是实数；命题 q ：正数的对数都是负数，则下列命题中为真命题的是（　）

A、 $(\neg p) \lor q$ B、 $p \land q$ C、 $(\neg p) \land (\neg q)$ D、 $(\neg p) \lor (\neg q)$

查看试题解析
2. 设α ， β为两个不同的平面，m ， n为两条不同的直线， $m \subset α ， n \subset β$ ，有两个命题：p：若m∥n ，则α∥β；q：若m⊥ β ，则α⊥β ，那么( )

A、“p或q”是假命题 B、“p且q”是真命题 C、“非p或q”是假命题 D、“非p且q”是真命题

查看试题解析
3. 已知命题p：任意 $x \in R$ ， 2^x<3^x；命题q：存在 $x \in R$ ， x³=1-x² ，则下列命题中为真命题的是(　　)

A、p且q B、 $\neg p$ 且q C、p且﹁q D、﹁p且﹁q

查看试题解析
4. 已知命题p：x²+2x-3>0，命题q：5x-6>x² ，则 $\neg p$ 是 $\neg q$ 的　(　　)

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 若命题p是真命题，命题q是假命题，则(　　)

A、p∧q是真命题 B、p∨q是假命题 C、¬p是真命题 D、¬q是真命题

查看试题解析
6. 若命题p：0是偶数，命题q：2是3的约数，则下列结论中正确的是(　　)

A、“p∨q”为假 B、“p∨q”为真 C、“p∧q”为真 D、以上都不对

查看试题解析
7. 已知：命题p：“a=1是 $x > 0 ， x + \frac{a}{x} \geq 2$ 的充分必要条件”；命题q：“ $\exists x \in R ， x^{2} + x - 2 > 0$ ，”则下列结论错误的是 ( )

A、命题“p∧q”是真命题 B、命题“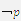（）∧q”是真命题 C、命题“p∧（ $\neg q$ ）”是真命题 D、命题“（ $\neg p$ )∧（ $\neg q$ ）”是真命题

查看试题解析
8. 下列命题：
①2>1或1<3；②方程x²－3x－4＝0的判别式大于或等于0；
③周长相等的两个三角形全等或面积相等的两个三角形全等；
④集合A∩B是集合A的子集，且是A∪B的子集．
其中真命题的个数是(　　)

A、1 B、2 C、3 D、4

查看试题解析
9. 已知命题p ， q,“非p”为假命题是“p或q” 为真命题的( )

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
10. 下列语句：① $\sqrt{3}$ 的值是无限循环小数；②x²>x；③△ABC的两角之和；④毕业班的学生．其中不是命题的是(　　)

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
11. 已知命题p：若实数x ， y满足x²＋y²＝0，则x ， y全为0；命题q：若a>b ，则 $\frac{1}{a}$ < $\frac{1}{b}$ ，给出下列四个命题：①p∧q；②p∨q；③ $\neg$ p；④ $\neg$ q.
其中真命题是（）．

A、①② B、②③ C、①④ D、②④

查看试题解析
12. 设P：函数f(x)=2^|x-a|在区间(4，+∞]上单调递增；q：log_a2＜1.如果“非p”是真命题，“p或q”也是真命题，那么实数a的取值范围是（）．

A、 $(- \infty ， 4)$ B、 $(- \infty ， 4]$ C、 $(4 ， + \infty)$ D、 $[4 ， + \infty)$

查看试题解析
13. 已知P：x²-x-6<0， q：x²>1，若“p且q”为真命题，试求x的取值范围（）.

A、{x|-2<x<-1} B、{x|1<x<3} C、{x|-2<x<-1或1<x<3} D、{ $x | - 2 \leq x < - 1$ 或 $1 \leq x \leq 3$ }

查看试题解析
14. 已知命题 p ：函数f(x)=log_0.5^(3-x) 的定义域为 $(- \infty ， 3)$ ；命题 q ：若 k<0 则函数 $h (x) = \frac{k}{x}$ 在 $(0 ， + \infty)$ 上是减函数，则下列结论：
①命题“p且q”为真；②命题“p或 $\neg q$ ”为假；③命题“p或q”为假；
④命题“ $\neg p$ 且 $\neg q$ ”为假，其中错误的是（）

A、①②③④ B、①②③ C、②④ D、①②

查看试题解析
15. 已知p：关于x的不等式x²+2ax+4>0对一切 $x \in R$ 恒成立；q：函数f(x)=-(5-2a)^x在R上是减函数.若“p或q”为真，“p且q”为假，求实数a的取值范围（）。

A、 $a \leq - 2$ B、 $a < - 2$ C、a>-2 D、a≥-2

查看试题解析

二、填空题

16. 已知命题 $P ： \forall x \in [0 ， \frac{π}{2}] ， \sin x < x$ ，那么命题 $\neg P$ 是.

查看试题解析
17. 已知命题 $p ： \exists x \in R ， x^{2} + \frac{1}{x^{2}} \leq 2$ ，命题q是命题p的否定，则命题p ， q ， p∧q ， p∨q中是真命题的是.

查看试题解析
18. 命题p：菱形的对角线互相垂直，则p的否命题是， $\neg$ p是．

查看试题解析
19. 已知命题p：(x＋2)(x－6)≤0，命题q：－3≤x≤7，若“p或q”为真命题，“p且q”为假命题，则实数x的取值范围为．

查看试题解析
20. 已知命题p：|3x-4|>2 ，命题q： $\frac{1}{x^{2} - x - 2} > 0$ ，求 $\neg$ p和 $\neg$ q对应的x的取值范围．

查看试题解析

三、解答题

21.
将下列命题写成“p或q”“p且q”和“ 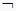p”的形式：

(1)、p：菱形的对角线互相垂直，q：菱形的对角线互相平分；

(2)、p：能被5整除的整数的个位数一定为5，q：能被5整除的整数的个位数一定为0.

查看试题解析
22. 已知命题 $p ： |x^{2} - x| \geq 6$ $q ： x \in z$ ，且“p且q”与“非q”同时为假命题，求x的值.

查看试题解析
23. 已知命题p：lg(x²－2x－2)≥0；命题q：0<x<4.若p且q为假，p或q为真，求实数x的取值范围．

查看试题解析
24. 写出下列各组命题构成的“p或q”、“p且q”以及“非p”形式的命题，并判断它们的真假．

(1)、 $\sqrt{5}$ 是有理数，q： $\sqrt{5}$ 是整数；

(2)、不等式x²－2x－3>0的解集是(－∞，－1)，q：不等式x²－2x－3>0的解集是(3，＋∞)．

查看试题解析
25. 已知命题 p：方程 $a^{2} x^{2} + a x - 2 = 0 ；$ 在 $[- 1 ， 1]$ 上有且仅有一解；命题 q ：只有一个实数x满足不等式 $x^{2} + 2 a x + 2 a \leq 0$ .若命题“ p 或q ”是假命题，求a的取值范围．

查看试题解析