初中数学人教版九年级下学期 第二十七章测试卷
试卷更新日期：2019-11-27 类型：单元试卷
一、单选题
-
1. 如图，l1∥l2∥l3 ， AC、DF交于点O，则下列比例中成立的是（ ）
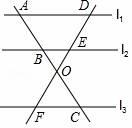A、 B、 C、 D、2. 如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且DE∥BC，EF∥AB．若 AD=2BD，则 的值为（ ）
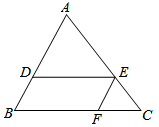A、 B、
C、
D、
3. 若 = ，则 的值为 （ ）A、1· B、
C、
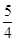D、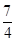
4. 如图，在 中， ， ， 为 边上的一点，且 ．若 的面积为 ，则 的面积为（ ）
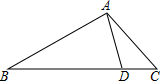A、 B、 C、 D、5. 如图，在 ABCD中，点E在对角线BD上，EM∥AD，交AB于点M，EN∥AB，交AD于点N，则下列式子一定正确的是( ）．
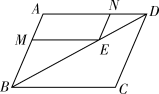A、 B、 C、 D、6. 如图，在科Rt△ABC中，∠ACB=90°，AC=6，BC=12，点D在边BC上，点E在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G，若EF=EG，则CD的长为（ ）
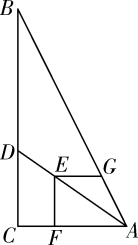A、3.6 B、4 C、4.8 D、57. 下列命题是真命题的是（ ）A、如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为2:3； B、如果两个三角形相似，相似比为4:9，那么这两个三角形的周长比为4:9； C、如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为2:3； D、如果两个三角形相似，相似比为4:9，那么这两个三角形的面积比为4:9.8. 如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上。若测得BE=20m，EC=10m，CD=20m，则河的宽度AB等于（ ）
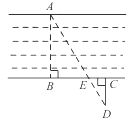A、60m B、40m C、30m D、20m9. 如图，在矩形ABCD中，E，F分别是AD，AB边上的点，连接CE，DF，他们相交于点G，延长CE交BA的延长线于点H，则图中的相似三角形共有（ ）
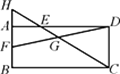A、5对 B、4对 C、3对 D、2对二、填空题
-
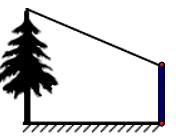
10. 小明想测量一棵树的高度，他发现树的影子恰好落在地面和一躲墙上，如图，此时测得地面上的影长为8米，墙上的影长为4米．同一时刻，一根长为1米且垂直于地面放置的标杆在地面上的影长为2米，则树的高度为。
11. 如图，在平面直角坐标系中，已知点A（﹣2，4），B（﹣4，﹣2），以原点O为位似中心，相似比为 ，把△ABO缩小，则点A的对应点A'的坐标是.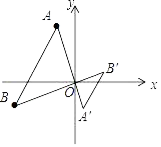
12. 观察下列的图形（a）﹣（g），其中哪些是与图形（1）、（2）或（3）相似的．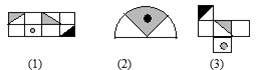
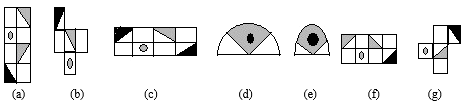
与图形（1）相似的有；（填序号）
与图形（2）相似的有；（填序号）
与图形（3）相似的有 ． （填序号）
三、综合题
-
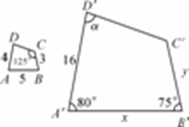
13. 在如图所示的两个相似的四边形中，求x ， y ， ∠α的值．
14. 如图，是小亮晚上在广场散步的示意图，图中线段AB表示站立在广场上的小亮，身高为1.6m，线段PO表示直立在广场上的灯杆，点P表示照明灯的位置．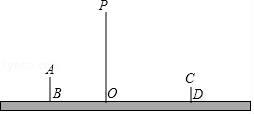
(1)、在小亮由B处沿BO所在的方向行走到达O处的过程中，他在地面上的影子长度越来越（用“长”或“短”填空）；请你在图中分别画出小亮站在B处、D处的影子；(2)、当小亮离开灯杆的距离OB＝3.6m时，小亮的影长为1.2m，灯杆的高度为多少m？(3)、当小亮离开灯杆的距离OD＝6m时，小亮的影长变为多少m？15. 如图，已知O是坐标原点，B、C两点的坐标分别为（3，﹣1）、（2，1）．
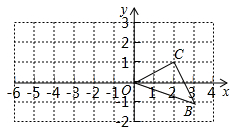(1)、以0点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；(2)、分别写出B、C两点的对应点B′、C′的坐标；(3)、如果△OBC内部一点M的坐标为（x，y），写出M的对应点M′的坐标．