初中数学浙教版七年级上册6.4 线段的和差 强化提升训练
试卷更新日期：2019-11-27 类型：同步测试
一、单选题
-
1. 如图，点C是AB的中点，点D是BC的中点，现给出下列等式：①CD=AC-DB，②CD= AB，③CD=AD-BC，④BD=2AD-AB.其中正确的等式编号是（ ）
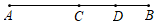A、 B、 C、 D、2. 已知点C是线段AB延长线上的一点，M、N分别是线段AB、AC的中点，若MN=4cm，且AB= AC，则线段AC的长为（ ）cmA、24 B、32 C、40 D、483. 已知线段AB=8，延长线段AB至C，使得BC= AB，延长线段BA至D，使得AD= AB，则下列判断正确的是（ ）A、BC= AD B、BD=3BC C、BD=4AD D、AC=6AD4. 已知线段 AB＝10cm，直线 AB 上有一点 C，且 BC＝4cm，M 是线段 AC 的中点，则 AM 的长（ ）A、7cm B、3cm C、3cm 或 7cm D、7cm 或 9cm5. 已知，如图，B，C 两点把线段 AD 分成 2：5：3 三部分，M 为 AD 的中点，BM=6cm，则 AD 的长为（ ）
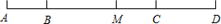A、21cm B、20cm C、19cm D、18cm6. 已知平面内有A，B，C三点，且线段 ，那么AC两点之间的距离为（ ）A、1cm B、6cm C、1cm或6cm D、无法确定7. 如图，ABCD是正方形场地，点E在DC的延长线上，AE与BC相交于点F．有甲、乙、丙三名同学同时从点A出发，甲沿着A—B—F—C的路径行走至C，乙沿着A—F—E—C—D的路径行走至D，丙沿着A—F—C—D的路径行走至D．若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序（由先至后）是（ ）
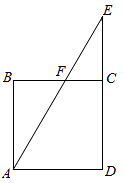A、甲、乙、丙 B、甲、丙、乙 C、乙、丙、甲 D、丙、甲、乙8. 如图，线段AB和线段CD的重合部分CB的长度是线段AB长的 ，M、N分别是线段AB和线段CD的中点，AB=18，MN=13，则线段AD的长为（ ）
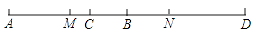A、31 B、33 C、32 D、34二、填空题
-
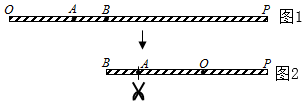
9. 如图1，OP为一条拉直的细线，长为7cm，A，B两点在OP上，若先握住点B，将OB折向BP，使得OB重叠在BP上，如图 再从图2的A点及与A点重叠处一起剪开，使得细线分成三段 若这三段的长度由短到长之比为1：2：4，其中以点P为一端的那段细线最长，则OB的长为cm.
10. 已知A，B，C三点都在直线l上，AC与BC的长度之比为2：3，D是AB的中点．若AC=4cm，则CD的长为cm．11. 如图，线段AB上有E，D，C，F四点，点E是线段AC的中点，点F是线段DB的中点，有下列结论： ① ② ③ ④ 其中正确的结论是（填相应的序号）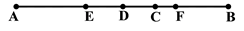
12. 如图，在数轴上，点A，B分别表示-15，9，点P，Q分别从点A，B同时开始沿数轴正方向运动，点P的速度是每秒3个单位，点Q的速度是每秒1个单位，运动时间为t秒．在运动过程中，当点P，点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点时，t的值是 ．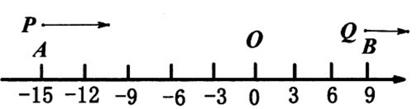
三、解答题
