2017年湖南省永州市冷水滩区中考数学一模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣2017的绝对值是( )A、2017 B、 C、﹣2017 D、﹣2. 下列运算正确的是( )A、a+a=2a2 B、a2•a3=a6 C、a3÷a=3 D、(﹣a)3=﹣a33. 不论a,b为何实数,a2+b2﹣2a﹣4b+7的值是( )A、总是正数 B、总是负数 C、可以是零 D、可以是正数也可以是负数4. 若关于x的一元二次方程x2+(k+3)x+2=0的一个根是﹣1,则另一个根是( )A、1 B、0 C、2 D、﹣25. 一个菱形被一条直线分成面积为x,y的两部分,则y与x之间的函数图象只可能是( )A、
 B、
B、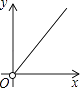 C、
C、 D、
D、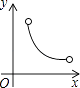 6. 如果事件A发生的概率是 ,那么在相同条件下重复试验,下列4种陈述中,不正确的有
6. 如果事件A发生的概率是 ,那么在相同条件下重复试验,下列4种陈述中,不正确的有①说明做100次这种试验,事件A必发生1次
②说明事件A发生的频率是
③说明做100次这种试验中,前99次事件A没发生,后1次事件A才发生
④说明做100次这种试验,事件A可能发生1次( )
A、①、②、③ B、①、②、④ C、②、③、④ D、①、②、③、④7. 如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( ) A、 B、 C、 D、8. 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )
A、 B、 C、 D、8. 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )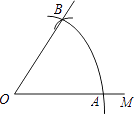 A、 B、 C、 D、9. 如图,Rt△ABC中,∠C=90°,AC=4,BC=4 ,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
A、 B、 C、 D、9. 如图,Rt△ABC中,∠C=90°,AC=4,BC=4 ,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )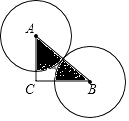 A、2π B、4π C、6π D、8π10. 已知,直线MN是等边△ABC底边BC的中垂线,点P在直线MN上,且使△PAB、△PAC、△PBC都是等腰三角形,满足上述条件的点P的个数有( )A、1个 B、2个 C、3个 D、4个11. 中国古代数学家杨辉的《田亩比类乘除捷法》有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?经过计算,你的结论是:长比宽多( )A、12步 B、24步 C、36步 D、48步12. 如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.
A、2π B、4π C、6π D、8π10. 已知,直线MN是等边△ABC底边BC的中垂线,点P在直线MN上,且使△PAB、△PAC、△PBC都是等腰三角形,满足上述条件的点P的个数有( )A、1个 B、2个 C、3个 D、4个11. 中国古代数学家杨辉的《田亩比类乘除捷法》有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?经过计算,你的结论是:长比宽多( )A、12步 B、24步 C、36步 D、48步12. 如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.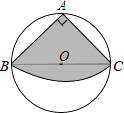 A、4 B、5 C、 D、2
A、4 B、5 C、 D、2二、填空题
-
13. ﹣ 的立方根是 .14. 若实数a、b满足a+b=﹣2,a2b+ab2=﹣10,则ab的值是 .15. 若∠α补角是∠α余角的3倍,则∠α= .16. 国家统计局数据显示,2016年我国GDP增速为6.7%,全年国内生产总值为744127亿元,“744127亿元”用科学记数法表示为亿元(保留五位有效数字)17. 某个立体图形的侧面展开图形如图所示,它的底面是正三角形,这个立体图形一定是 .
 18. 已知某抛物线的顶点坐标为(﹣2,1),且与y轴相交于点(0,4),这个抛物线所表示的二次函数的表达式是 .19. 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是 , △ABC的面积为 .
18. 已知某抛物线的顶点坐标为(﹣2,1),且与y轴相交于点(0,4),这个抛物线所表示的二次函数的表达式是 .19. 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是 , △ABC的面积为 . 20.
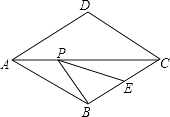
20.如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为 .
三、解答题
-
21. 计算:|1﹣ |+(2017﹣50 )0+( )﹣1 .22. 已知反比例函数y= 和一次函数y=﹣x+a﹣2(a为常数)(1)、当a=0时,求反比例函数与一次函数的交点坐标.(2)、当反比例函数与一次函数有两个交点时,请确定a的范围.23.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.
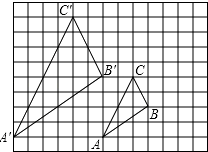 (1)、求证:△ABC∽A′B′C′;(2)、A′B′C′与△ABC是位似图形吗?如果是,在图形上画出位似中心并求出位似比.24.
(1)、求证:△ABC∽A′B′C′;(2)、A′B′C′与△ABC是位似图形吗?如果是,在图形上画出位似中心并求出位似比.24.某市中考体育测试有“跳绳”项目,为加强训练,某班女生分成甲、乙两组参加班级跳绳对抗赛,两组参赛人数相等,比赛结束后,依据两组学生的成绩(满分为10分)绘制了如下统计图表:
甲组学生成绩统计表
分 数
人 数
5分
5人
6分
2人
7分
3人
8分
1人
9分
4人
 (1)、经计算,乙组的平均成绩为7分,中位数是6分,请求出甲组学生的平均成绩、中位数,并从平均数的角度分析哪个组的成绩较好?(2)、经计算,甲组的成绩的方差是2.56,乙组的方差是多少?比较可得哪个组的成绩较为整齐?(3)、学校组织跳绳比赛,班主任决定从这次对抗赛中得分为9分的学生中抽签选取5个人组成代表队参赛,则在对抗赛中得分为9分的学生参加比赛的概率是多少?25. 如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)、经计算,乙组的平均成绩为7分,中位数是6分,请求出甲组学生的平均成绩、中位数,并从平均数的角度分析哪个组的成绩较好?(2)、经计算,甲组的成绩的方差是2.56,乙组的方差是多少?比较可得哪个组的成绩较为整齐?(3)、学校组织跳绳比赛,班主任决定从这次对抗赛中得分为9分的学生中抽签选取5个人组成代表队参赛,则在对抗赛中得分为9分的学生参加比赛的概率是多少?25. 如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E. (1)、求证:DE是⊙O的切线.(2)、求DE的长.26.
(1)、求证:DE是⊙O的切线.(2)、求DE的长.26.如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
 (1)、用含x的代数式表示BQ、BP的长度,并求x的取值范围.(2)、设四边形APQC的面积为y(cm2),求y与x的函数关系式?(3)、是否存在这样的x,使得四边形APQC的面积是△ABC面积的 ?如果存在,求出x的值;不存在请说明理由.27.
(1)、用含x的代数式表示BQ、BP的长度,并求x的取值范围.(2)、设四边形APQC的面积为y(cm2),求y与x的函数关系式?(3)、是否存在这样的x,使得四边形APQC的面积是△ABC面积的 ?如果存在,求出x的值;不存在请说明理由.27.问题探究:
【1】新知学习
⑴梯形的中位线:连接梯形两腰中点的线段叫做梯形的中位线.
⑵梯形的中位线性质:梯形的中位线平行于两底,并且等于两底和的一半.
⑶形如分式 (m为常数,且m>0),若x>0,则 ,并且有下列结论:
当x 逐渐增大时,分母x+2m逐渐增大,分式 的值逐渐减少并趋于0,但仍大于0.当x 逐渐减少时,分母x+2m逐渐减少,分式 的值逐渐增大并趋于 ,即趋于 ,但仍小于 .
【2】问题解决
如图2,已知在梯形ABCD中,AD∥BC,AD<BC,E、F分别是AB、CD的中点.
 (1)、设AD=7,BC=17,求 的值.(2)、设AD=a(a为正的常数),BC=x,请问:当BC的长不断增大时, 的值能否大于或等于3,试证明你的结论.(3)、
(1)、设AD=7,BC=17,求 的值.(2)、设AD=a(a为正的常数),BC=x,请问:当BC的长不断增大时, 的值能否大于或等于3,试证明你的结论.(3)、进一步猜想:任何一个梯形的中位线所分成的两部分图形的面积的比值所在的范围是什么,并说明理由.
