2017年湖南省永州市冷水滩区中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 2017的相反数是( )A、2017 B、﹣2017 C、 D、﹣2. 下列各式计算正确的是( )A、6a+2a=8a2 B、(a﹣b)2=a2﹣b2 C、a4•a6=a10 D、(a3)2=a53. 不等式组 的解集在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、 4. 下列命题中错误的是( )A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直 C、同旁内角互补 D、矩形的对角线相等5. 下列说法正确的是( )A、要了解我市九年级学生的身高,应采用普查的方式 B、若甲队成绩的方差为5,乙队成绩的方差为3,则甲队成绩不如乙队成绩稳定 C、如果明天下雨的概率是99%,那么明天一定会下雨 D、一组数据4,6,7,6,7,8,9的中位数和众数都是66.
4. 下列命题中错误的是( )A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直 C、同旁内角互补 D、矩形的对角线相等5. 下列说法正确的是( )A、要了解我市九年级学生的身高,应采用普查的方式 B、若甲队成绩的方差为5,乙队成绩的方差为3,则甲队成绩不如乙队成绩稳定 C、如果明天下雨的概率是99%,那么明天一定会下雨 D、一组数据4,6,7,6,7,8,9的中位数和众数都是66.下列四个立体图形中,左视图为矩形的是( )
 A、①③ B、①④ C、②③ D、③④7. 如图,反比例函数y= 的图象与一次函数y=﹣ x的图象交于点A(﹣2,m)和点B,则点B的坐标是( )
A、①③ B、①④ C、②③ D、③④7. 如图,反比例函数y= 的图象与一次函数y=﹣ x的图象交于点A(﹣2,m)和点B,则点B的坐标是( )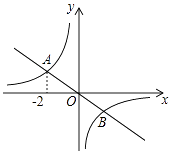 A、(2,﹣1) B、(1,﹣2) C、( ,﹣1) D、(1,﹣ )8.
A、(2,﹣1) B、(1,﹣2) C、( ,﹣1) D、(1,﹣ )8.如图,挂在弹簧称上的长方体铁块浸没在水中,提着弹簧称匀速上移,直至铁块浮出水面停留在空中(不计空气阻力),弹簧称的读数F(N)与时间t(s)的函数图象大致是( )
 A、
A、 B、
B、 C、
C、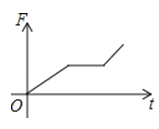 D、
D、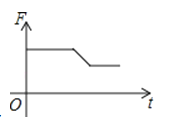 9. 如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( )
9. 如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 抛物线y=3(x﹣2)2+5的顶点坐标是 .11. 已知关于x的一元二次方程2x2﹣3kx+4=0的一个根是1,则k= .12. 若a2﹣3a+1=0,则 = .13. 如图,AB=AC,要使△ABE≌△ACD,应添加的条件是(添加一个条件即可).
 14. 如图,在△ABC中,DE∥BC, = ,△ADE的面积是8,则△ABC的面积为 .
14. 如图,在△ABC中,DE∥BC, = ,△ADE的面积是8,则△ABC的面积为 . 15. 杨辉是我国南宋末年的一位杰出的数学家.在他著的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角”,它是杨辉的一大重要研究成果.
15. 杨辉是我国南宋末年的一位杰出的数学家.在他著的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角”,它是杨辉的一大重要研究成果.我们把杨辉三角的每一行分别相加,如下:
1 ( 1 )
1 1 ( 1+1=2 )
1 2 1 (1+2+1=4 )
1 3 3 1 (1+3+3+1=8 )
1 4 6 4 1 (1+4+6+4+1=16 )
1 5 10 10 5 1 (1+5+10+10+5+1=32 )
1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 )
…写出杨辉三角第n行中n个数之和等于 .
16. 一个不透明的盒子中装有3个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为 .17. 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= (x<0)的图象经过点A,若S△ABO= ,则k的值为 .
三、解答题
-
18. 计算:(π﹣3)0﹣(﹣1)2017+(﹣ )﹣2+tan60°+| ﹣2|19. 先化简,再求值:( )÷ ,其中a=3.20. 在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类
频数
百分比
A.科普类
12
30%
B.文学类
n
35%
C.艺术类
m
20%
D.其它类
6
15%
 (1)、统计表中的n= , 并补全条形统计图;(2)、本次活动师生共捐书2000本,请估计有多少本科普类图书?21. 测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)、统计表中的n= , 并补全条形统计图;(2)、本次活动师生共捐书2000本,请估计有多少本科普类图书?21. 测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2) (1)、若已知CD=20米,求建筑物BC的高度;(2)、若已知旗杆的高度AB=5米,求建筑物BC的高度.22. 某实验学校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.(1)、求两人学习桌和三人学习桌的单价;(2)、学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.23. 如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)、若已知CD=20米,求建筑物BC的高度;(2)、若已知旗杆的高度AB=5米,求建筑物BC的高度.22. 某实验学校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.(1)、求两人学习桌和三人学习桌的单价;(2)、学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.23. 如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC. (1)、求证:△AEF≌△DCE;(2)、若CD=1,求BE的长.24. 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)、求证:△AEF≌△DCE;(2)、若CD=1,求BE的长.24. 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE. (1)、求证:BC是⊙O的切线;(2)、若tan∠G= ,BE=4,求⊙O的半径;(3)、在(2)的条件下,求AP的长.25. 如图,抛物线y= x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
(1)、求证:BC是⊙O的切线;(2)、若tan∠G= ,BE=4,求⊙O的半径;(3)、在(2)的条件下,求AP的长.25. 如图,抛物线y= x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C; (1)、求该抛物线的解析式;(2)、求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)、点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)、点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.