2017年湖南省娄底市中考数学一模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣3的相反数是( )A、 B、 C、3 D、﹣32. 我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示这个数字是( )A、6.75×103吨 B、67.5×103吨 C、6.75×104吨 D、6.75×105吨3. 下列运算正确的是( )A、a2•a3=a6 B、(ab)2=a2b2 C、(a2)3=a5 D、a2+a2=a44. 以下图形中对称轴的数量小于3的是( )A、
 B、
B、 C、
C、 D、
D、 5. 已知点M(1﹣2m,m﹣1)在第四象限,则m的取值范围在数轴上表示正确的是( )A、
5. 已知点M(1﹣2m,m﹣1)在第四象限,则m的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、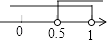 D、
D、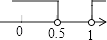 6. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )A、560(1+x)2=315 B、560(1﹣x)2=315 C、560(1﹣2x)2=315 D、560(1﹣x2)=3157. 将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )A、96 B、69 C、66 D、998. 在下列条件中,不能判定四边形为平行四边形的是( )A、一组对边平行,另一组对边相等 B、一组对边平行且相等 C、两组对边分别平行 D、对角线互相平分9. 点(2,﹣4)在反比例函数y= 的图象上,则下列各点在此函数图象上的是( )A、(2,4) B、(﹣1,﹣8) C、(﹣2,﹣4) D、(4,﹣2)10. 如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )
6. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )A、560(1+x)2=315 B、560(1﹣x)2=315 C、560(1﹣2x)2=315 D、560(1﹣x2)=3157. 将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )A、96 B、69 C、66 D、998. 在下列条件中,不能判定四边形为平行四边形的是( )A、一组对边平行,另一组对边相等 B、一组对边平行且相等 C、两组对边分别平行 D、对角线互相平分9. 点(2,﹣4)在反比例函数y= 的图象上,则下列各点在此函数图象上的是( )A、(2,4) B、(﹣1,﹣8) C、(﹣2,﹣4) D、(4,﹣2)10. 如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )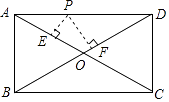 A、增大 B、减小 C、不变 D、先增大再减小
A、增大 B、减小 C、不变 D、先增大再减小二、填空题
-
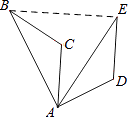
11. 使式子 有意义的x取值范围是 .12. 从数字2,3,4中任选两个数组成一个两位数,组成的数是偶数的概率是 .13. 若一次函数y=﹣2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是(写出一个即可).14. 如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE= .
 15. 将一张长方形纸片折叠成如图所示的形状,则∠ABC的度数 .
15. 将一张长方形纸片折叠成如图所示的形状,则∠ABC的度数 .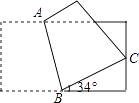 16.
16.如图,下列各图形中的三个数之间均具有相同的规律,依此规律,那么第100个图形中的x= .

三、解答题
-
17. 计算:( )﹣1﹣(2017﹣π)0﹣2sin45°+| ﹣1|18. 已知4x=3y,求代数式(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2的值.
四、解答题
-
19.
我市某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为A、B、C、D、E、五个组,x表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
A组:90≤x≤100 B组:80≤x<90 C组:70≤x<80 D组:60≤x<70 E组:x<60
 (1)、参加调查测试的学生共有人;请将两幅统计图补充完整 .(2)、本次调查测试成绩的中位数落在组内.(3)、本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?20. 放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ≈1.414, ≈1.732,最后结果精确到1米).
(1)、参加调查测试的学生共有人;请将两幅统计图补充完整 .(2)、本次调查测试成绩的中位数落在组内.(3)、本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?20. 放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ≈1.414, ≈1.732,最后结果精确到1米). 21. 目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?22. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.
21. 目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?22. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF.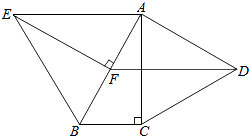 (1)、求证:△ABC≌△EAF;(2)、试判断四边形EFDA的形状,并证明你的结论.23. 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)、求证:△ABC≌△EAF;(2)、试判断四边形EFDA的形状,并证明你的结论.23. 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,BC=6, .求BE的长.24.
(1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,BC=6, .求BE的长.24.如图1(注:与图2完全相同),二次函数y= x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
 (1)、求该二次函数的解析式;(2)、设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)、若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
(1)、求该二次函数的解析式;(2)、设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)、若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).