江苏省泰州市2019年中考数学试卷
试卷更新日期:2019-11-27 类型:中考真卷
一、单选题
-
1. -1的相反数是( )A、 B、-1 C、0 D、12. 如图图形中的轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 3. 方程 的两根为 、 ,则 等于( )A、-6 B、6 C、-3 D、34. 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
3. 方程 的两根为 、 ,则 等于( )A、-6 B、6 C、-3 D、34. 小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A、20 B、300 C、500 D、8005. 如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是( )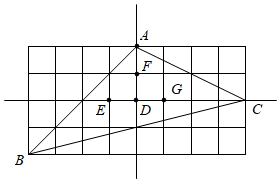 A、点 B、点 C、点 D、点6. 若 ,则代数式 的值为( )A、-1 B、1 C、2 D、3
A、点 B、点 C、点 D、点6. 若 ,则代数式 的值为( )A、-1 B、1 C、2 D、3二、填空题
-
7. 计算: .8. 若分式 有意义,则 的取值范围是 .9. 2019年5月28日,我国“科学”号远洋科考船在最深约为 的马里亚纳海沟南侧发现了近10片珊瑚林.将11000用科学记数法表示为 .10. 不等式组 的解集为 .11. 八边形的内角和为度.12. 命题“三角形的三个内角中至少有两个锐角”是(填“真命题”或“假命题”).13. 根据某商场2018年四个季度的营业额绘制成如图所示的扇形统计图,其中二季度的营业额为1000万元,则该商场全年的营业额为万元.
 14. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .15. 如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为cm.
14. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .15. 如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为cm. 16. 如图, 的半径为5,点 在 上,点 在 内,且 ,过点 作 的垂线交 于点 、 .设 , ,则 与 的函数表达式为 .
16. 如图, 的半径为5,点 在 上,点 在 内,且 ,过点 作 的垂线交 于点 、 .设 , ,则 与 的函数表达式为 .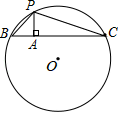
三、解答题
-
17.(1)、计算: ;(2)、解方程: .18. 是指空气中直径小于或等于 的颗粒物,它对人体健康和大气环境造成不良影响,下表是根据《全国城市空气质量报告》中的部分数据制作的统计表.根据统计表回答下列问题,
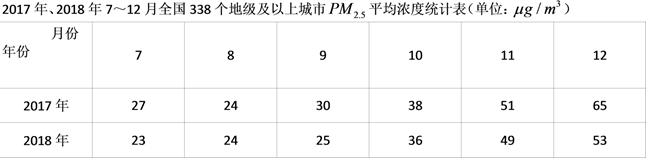 (1)、2018年7~12月 平均浓度的中位数为 ;(2)、“扇形统计图”和“折线统计图”中,更能直观地反映2018年7~12月 平均浓度变化过程和趋势的统计图是;(3)、某同学观察统计表后说:“2018年7~12月与2017年同期相比,空气质量有所改善”,请你用一句话说明该同学得出这个结论的理由.19. 小明代表学校参加“我和我的祖国”主题宣传教育活动.该活动分为两个阶段,第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目(依次用 、 、 表示),第二阶段有“故事演讲”、“诗歌朗诵”2个项目(依次用 、 表示),参加人员在每个阶段各随机抽取一个项目完成.用画树状图或列表的方法列出小明参加项目的所有等可能的结果,并求小明恰好抽中 、 两个项目的概率.20. 如图, 中, , , .
(1)、2018年7~12月 平均浓度的中位数为 ;(2)、“扇形统计图”和“折线统计图”中,更能直观地反映2018年7~12月 平均浓度变化过程和趋势的统计图是;(3)、某同学观察统计表后说:“2018年7~12月与2017年同期相比,空气质量有所改善”,请你用一句话说明该同学得出这个结论的理由.19. 小明代表学校参加“我和我的祖国”主题宣传教育活动.该活动分为两个阶段,第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目(依次用 、 、 表示),第二阶段有“故事演讲”、“诗歌朗诵”2个项目(依次用 、 表示),参加人员在每个阶段各随机抽取一个项目完成.用画树状图或列表的方法列出小明参加项目的所有等可能的结果,并求小明恰好抽中 、 两个项目的概率.20. 如图, 中, , , .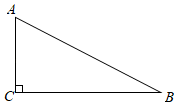 (1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.21. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .
(1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.21. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .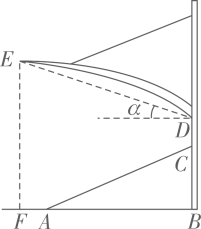
求:
(1)、观众区的水平宽度 ;(2)、顶棚的 处离地面的高度 .( , ,结果精确到 )22. 如图,在平面直角坐标系 中,二次函数图象的顶点坐标为 ,该图象与 轴相交于点 、 ,与 轴相交于点 ,其中点 的横坐标为1.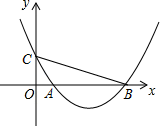 (1)、求该二次函数的表达式;(2)、求 .23. 小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于 ,超过 时,所有这种水果的批发单价均为3元 .图中折线表示批发单价 (元 )与质量 的函数关系.
(1)、求该二次函数的表达式;(2)、求 .23. 小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于 ,超过 时,所有这种水果的批发单价均为3元 .图中折线表示批发单价 (元 )与质量 的函数关系. (1)、求图中线段 所在直线的函数表达式;(2)、小李用800元一次可以批发这种水果的质量是多少?24. 如图,四边形 内接于 , 为 的直径, 为 的中点,过点 作 ,交 的延长线于点 .
(1)、求图中线段 所在直线的函数表达式;(2)、小李用800元一次可以批发这种水果的质量是多少?24. 如图,四边形 内接于 , 为 的直径, 为 的中点,过点 作 ,交 的延长线于点 . (1)、判断 与 的位置关系,并说明理由;(2)、若 的半径为5, ,求 的长.25. 如图,线段 ,射线 , 为射线 上一点,以 为边作正方形 ,且点 、 与点 在 两侧,在线段 上取一点 ,使 ,直线 与线段 相交于点 (点 与点 、 不重合).
(1)、判断 与 的位置关系,并说明理由;(2)、若 的半径为5, ,求 的长.25. 如图,线段 ,射线 , 为射线 上一点,以 为边作正方形 ,且点 、 与点 在 两侧,在线段 上取一点 ,使 ,直线 与线段 相交于点 (点 与点 、 不重合).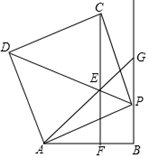 (1)、求证: ;(2)、判断 与 的位置关系,并说明理由;(3)、求 的周长.26. 已知一次函数 和反比例函数 .
(1)、求证: ;(2)、判断 与 的位置关系,并说明理由;(3)、求 的周长.26. 已知一次函数 和反比例函数 .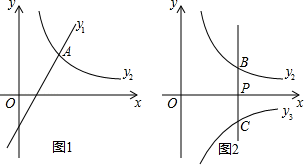 (1)、如图1,若 ,且函数 、 的图象都经过点 .
(1)、如图1,若 ,且函数 、 的图象都经过点 .①求 , 的值;
②直接写出当 时 的范围;
(2)、如图2,过点 作 轴的平行线 与函数 的图象相交于点 ,与反比例函数 的图象相交于点 .①若 ,直线 与函数 的图象相交点 .当点 、 、 中的一点到另外两点的距离相等时,求 的值;
②过点 作 轴的平行线与函数 的图象相交于点 .当 的值取不大于1的任意实数时,点 、 间的距离与点 、 间的距离之和 始终是一个定值.求此时 的值及定值 .