青海省2019年中考数学试卷
试卷更新日期:2019-11-27 类型:中考真卷
一、填空题(本大题共12小题15空,每空2分,共30分)
-
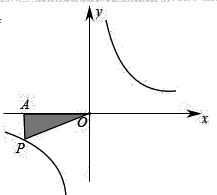
1. 的绝对值是; 的立方根是.2. 分解因式: ;分式方程 的解为.3. 世界科技不断发展,人们制造出的晶体管长度越来越短,某公司研发出长度只有0.000000006米的晶体管,该数用科学记数法表示为米.4. 某种药品原价每盒60元,由于医疗政策改革,价格经过两次下调后现在售价每盒48.6元,则平均每次下调的百分率为.5. 如图, 是反比例函数 图象上的一点,过点 向 轴作垂线交于点 ,连接 .若图中阴影部分的面积是1,则此反比例函数的解析式为.
 6. 如图,在直角坐标系中,已知点 ,将 绕点 逆时针方向旋转 后得到 ,则点 的坐标是.
6. 如图,在直角坐标系中,已知点 ,将 绕点 逆时针方向旋转 后得到 ,则点 的坐标是.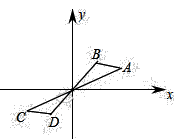 7. 如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据: 米, 米, , ,则 的长为米.(结果保留根号)
7. 如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据: 米, 米, , ,则 的长为米.(结果保留根号)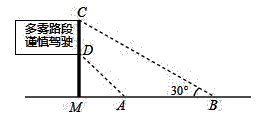 8. 一只不透明的布袋中有三种珠子(除颜色以外没有任何区别),分别是3个红珠子,4个白珠子和5个黑珠子,每次只摸出一个珠子,观察后均放回搅匀,在连续9次摸出的都是红珠子的情况下,第10次摸出红珠子的概率是.9. 如图是用杠杆撬石头的示意图, 是支点,当用力压杠杆的 端时,杠杆绕 点转动,另一端 向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的 端必须向上翘起 ,已知杠杆的动力臂 与阻力臂 之比为 ,要使这块石头滚动,至少要将杠杆的 端向下压 .
8. 一只不透明的布袋中有三种珠子(除颜色以外没有任何区别),分别是3个红珠子,4个白珠子和5个黑珠子,每次只摸出一个珠子,观察后均放回搅匀,在连续9次摸出的都是红珠子的情况下,第10次摸出红珠子的概率是.9. 如图是用杠杆撬石头的示意图, 是支点,当用力压杠杆的 端时,杠杆绕 点转动,另一端 向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的 端必须向上翘起 ,已知杠杆的动力臂 与阻力臂 之比为 ,要使这块石头滚动,至少要将杠杆的 端向下压 . 10. 根据如图所示的程序,计算 的值,若输入 的值是1时,则输出的 值等于.
10. 根据如图所示的程序,计算 的值,若输入 的值是1时,则输出的 值等于.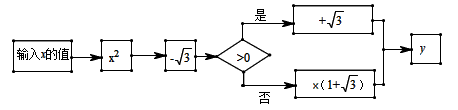 11. 如图在正方形 中,点 是以 为直径的半圆与对角线 的交点,若圆的半径等于1,则图中阴影部分的面积为.
11. 如图在正方形 中,点 是以 为直径的半圆与对角线 的交点,若圆的半径等于1,则图中阴影部分的面积为.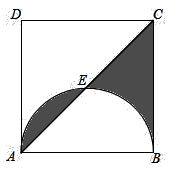 12. 如图,将图1中的菱形剪开得到图2,图中共有4个菱形;将图2中的一个菱形剪开得到图3,图中共有7个菱形;如此剪下去,第5图中共有个菱形 ,第 个图中共有个菱形.
12. 如图,将图1中的菱形剪开得到图2,图中共有4个菱形;将图2中的一个菱形剪开得到图3,图中共有7个菱形;如此剪下去,第5图中共有个菱形 ,第 个图中共有个菱形.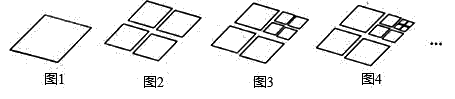
二、单项选择题(本大题共8小题,每小题3分,共24分)
-
13. 下面几何体中,俯视图为三角形的是( )A、
 B、
B、 C、
C、 D、
D、 14. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放:两个三角板的一直角边重合,含 角的三角板的斜边与纸条一边重合,含 角的三角板的一个顶点在纸条的另一边上,则 的度数是( )
14. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放:两个三角板的一直角边重合,含 角的三角板的斜边与纸条一边重合,含 角的三角板的一个顶点在纸条的另一边上,则 的度数是( )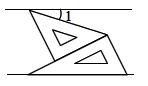 A、 B、 C、 D、15. 如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量分别为( )
A、 B、 C、 D、15. 如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量分别为( )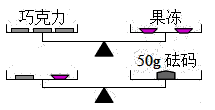 A、 , B、 , C、 , D、 ,16. 为了了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班50名学生进行了调查,有关数据如下表,这组数据的中位数和众数为( )
A、 , B、 , C、 , D、 ,16. 为了了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班50名学生进行了调查,有关数据如下表,这组数据的中位数和众数为( )每周做家务的时间
0
1
1.5
2
2.5
3
3.5
4
人数(人
2
2
6
8
12
13
4
3
A、2.5和2.5 B、2.25和3 C、2.5和3 D、10和1317. 如图,小莉从 点出发,沿直线前进10米后左转 ,再沿直线前进10米,又向左转 , ,照这样走下去,她第一次回到出发点 时,一共走的路程是( )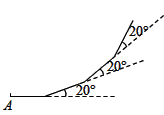 A、150米 B、160米 C、180米 D、200米18. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )
A、150米 B、160米 C、180米 D、200米18. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )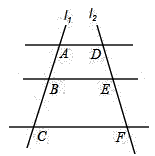 A、3.6 B、4.8 C、5 D、5,219. 如图,在扇形 中, 为弦, , , ,则 的长为( )
A、3.6 B、4.8 C、5 D、5,219. 如图,在扇形 中, 为弦, , , ,则 的长为( )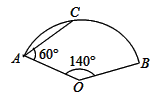 A、 B、 C、 D、20. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( )
A、 B、 C、 D、20. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( ) A、
A、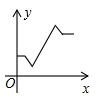 B、
B、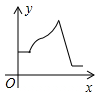 C、
C、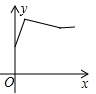 D、
D、
三、(本大题共3小题,第21题5分,第2题5分,第23题8分,共18分)
-
21. 计算:22. 化简求值: ;其中23. 如图,在 中, , 是 的中点, 是 的中点,过点 作 交 的延长线于点 ,连接 .
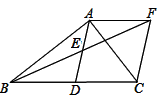 (1)、求证: ;(2)、证明四边形 是菱形.
(1)、求证: ;(2)、证明四边形 是菱形.四、(本大题共3小题,第24题9分,第25题8分,第26题9分,共26分)
-
24. 某市为了提升菜篮子工程质量,计划用大、中型车辆共30辆调拨不超过190吨蔬菜和162吨肉制品补充当地市场.已知一辆大型车可运蔬菜8吨和肉制品5吨;一辆中型车可运蔬菜3吨和肉制品6吨.(1)、符合题意的运输方案有几种?请你帮助设计出来;(2)、若一辆大型车的运费是900元,一辆中型车的运费为600元,试说明(1)中哪种运输方案费用最低?最低费用是多少元?25. 如图,在 中,点 、 分别是半径 、弦 的中点,过点 作 于点 .
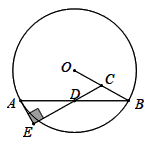 (1)、求证: 是 的切线;(2)、若 , ,求 的半径.26. “只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“ 、 、 、 ”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图)
(1)、求证: 是 的切线;(2)、若 , ,求 的半径.26. “只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“ 、 、 、 ”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图)血型统计表
血型
人数
10
5
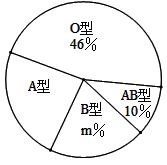 (1)、本次随机抽取献血者人数为人,图中 ;(2)、补全表中的数据;(3)、若这次活动中该校有1300人义务献血,估计大约有多少人是 型血?(4)、现有4个自愿献血者,2人为 型,1人为 型,1人为 型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为 型的概率.
(1)、本次随机抽取献血者人数为人,图中 ;(2)、补全表中的数据;(3)、若这次活动中该校有1300人义务献血,估计大约有多少人是 型血?(4)、现有4个自愿献血者,2人为 型,1人为 型,1人为 型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为 型的概率.五、(本大题共2小题,第27题10分,第28题12分,共22分)
-
27. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①
这是中国古代数学的瑰宝之一.
而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设 (周长的一半),则 ②
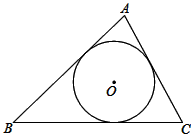 (1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .28. 如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点 、 、 三点.
(1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .28. 如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点 、 、 三点. (1)、求抛物线的解析式和对称轴;(2)、 是抛物线对称轴上的一点,求满足 的值为最小的点 坐标(请在图1中探索);(3)、在第四象限的抛物线上是否存在点 E ,使四边形 OEBF 是以 OB 为对角线且面积为12的平行四边形?若存在,请求出点 E 坐标,若不存在请说明理由(请在图2中探索)
(1)、求抛物线的解析式和对称轴;(2)、 是抛物线对称轴上的一点,求满足 的值为最小的点 坐标(请在图1中探索);(3)、在第四象限的抛物线上是否存在点 E ,使四边形 OEBF 是以 OB 为对角线且面积为12的平行四边形?若存在,请求出点 E 坐标,若不存在请说明理由(请在图2中探索)