浙江省杭州市富阳区富春中2019-2020学年八年级上学期数学9月月考试卷
试卷更新日期:2019-11-27 类型:月考试卷
一、单选题
-
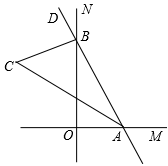
1. 图中钝角三角形有( )个.
 A、1 B、2 C、3 D、42. 下列四个图形中,线段BE是△ABC的高的是( )A、
A、1 B、2 C、3 D、42. 下列四个图形中,线段BE是△ABC的高的是( )A、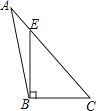 B、
B、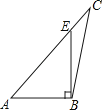 C、
C、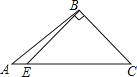 D、
D、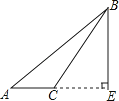 3. 下列各组线段中,能组成三角形的是( )A、4,6,10 B、3,6,7 C、5,6,12 D、2,3,64. 对于命题“如果∠1+∠2=90°,那么∠1=∠2”,能说明它是假命题的反例是( )A、∠1=60°,∠2=40° B、∠1=50°,∠2=40° C、∠1=∠2=40° D、∠1=∠2=45°5. 如图,△ABC 中,点 D,E,F 分别为线段 BC,AD,CE 的中点,且△AEC 的面积为 1,则△BEF 的面积为( )
3. 下列各组线段中,能组成三角形的是( )A、4,6,10 B、3,6,7 C、5,6,12 D、2,3,64. 对于命题“如果∠1+∠2=90°,那么∠1=∠2”,能说明它是假命题的反例是( )A、∠1=60°,∠2=40° B、∠1=50°,∠2=40° C、∠1=∠2=40° D、∠1=∠2=45°5. 如图,△ABC 中,点 D,E,F 分别为线段 BC,AD,CE 的中点,且△AEC 的面积为 1,则△BEF 的面积为( ) A、2 B、1 C、0.25 D、0.56. 如图,在△ABC 中,AE 是和 AF 分别是 BC 边上的中线和高线,AD 是∠BAC 的平分线.则下列线段中最短的是( )
A、2 B、1 C、0.25 D、0.56. 如图,在△ABC 中,AE 是和 AF 分别是 BC 边上的中线和高线,AD 是∠BAC 的平分线.则下列线段中最短的是( )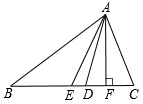 A、AE B、AD C、AF D、AC7. 根据下列条件,能作出唯一的△ABC 的是( )A、AB=7,BC=3,AC=3 B、∠A=30°,AC=4,BC=3 C、∠C=90°,∠B=50º D、BC=5,AC=7,AB=48. 如图,在△ABC 中,AB=AC,∠BAC 的角平分线与∠ABC 的角平分线交于点 D,若∠ADB=130°,∠C=( )
A、AE B、AD C、AF D、AC7. 根据下列条件,能作出唯一的△ABC 的是( )A、AB=7,BC=3,AC=3 B、∠A=30°,AC=4,BC=3 C、∠C=90°,∠B=50º D、BC=5,AC=7,AB=48. 如图,在△ABC 中,AB=AC,∠BAC 的角平分线与∠ABC 的角平分线交于点 D,若∠ADB=130°,∠C=( )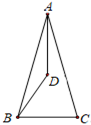 A、50° B、65° C、80° D、100°9. 如图,△ABC≌△AED,点 E 在线段 BC 上,∠1=48º,则∠AED 的度数是( )
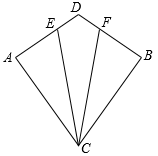
A、50° B、65° C、80° D、100°9. 如图,△ABC≌△AED,点 E 在线段 BC 上,∠1=48º,则∠AED 的度数是( )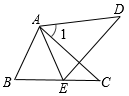 A、66° B、65° C、62° D、60°10. 如图,BF 是∠ABD 的平分线,CE 是∠ACD 的平分线,BF 与 CE 交于 G,若∠BDC=130°,∠BGC=100°,则∠A 的度数为( )
A、66° B、65° C、62° D、60°10. 如图,BF 是∠ABD 的平分线,CE 是∠ACD 的平分线,BF 与 CE 交于 G,若∠BDC=130°,∠BGC=100°,则∠A 的度数为( )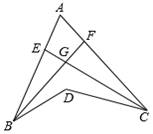 A、60° B、70° C、80° D、90°
A、60° B、70° C、80° D、90°二、填空题
-
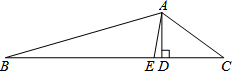
11. 已知三角形的两边长分别为 3 和 4,第三边长是奇数,则这个三角形的周长是12. 如图,AE是 的角平分线, 于点D , 若 , , 度
 13. 在三角形的三个内角中,锐角最多有个,至少有个.14. 三角形内到三条边距离相等的点是三条线的交点.15. 如图,在△ABC 中,AD 平分∠BAC,∠ADC=64º,∠B=3∠DAB.则∠C=.
13. 在三角形的三个内角中,锐角最多有个,至少有个.14. 三角形内到三条边距离相等的点是三条线的交点.15. 如图,在△ABC 中,AD 平分∠BAC,∠ADC=64º,∠B=3∠DAB.则∠C=.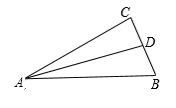 16. 如图,在 3×3 的正方形网格中标出了∠1 和∠2,则∠2-∠1=°
16. 如图,在 3×3 的正方形网格中标出了∠1 和∠2,则∠2-∠1=°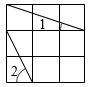
三、解答题
-
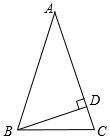
17. 如图,在△ABC 中,∠C=∠ABC=2∠A-10º,BD⊥AC 于 D,求∠DBC的度数.
 18. 已知:如图,在四边形 ABCD 中,AB=CD,AD=BC,EF 过BD 的中点 O.求证:OE=OF.
18. 已知:如图,在四边形 ABCD 中,AB=CD,AD=BC,EF 过BD 的中点 O.求证:OE=OF.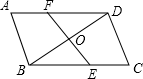 19. 如图,将△ABC 分别沿 AB,AC 翻折得到△ABD 和△AEC,线段 BD 与AE 交于点 F.
19. 如图,将△ABC 分别沿 AB,AC 翻折得到△ABD 和△AEC,线段 BD 与AE 交于点 F.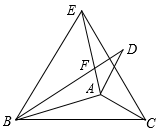 (1)、若∠ABC=16º,∠ACB=30°,求∠DAE 及∠BFE 的值;(2)、若 BD 与 CE 所在的直线互相垂直,求∠CAB 的度数.20. 如图,在△ABC 中,记∠A=x 度,回答下列问题:
(1)、若∠ABC=16º,∠ACB=30°,求∠DAE 及∠BFE 的值;(2)、若 BD 与 CE 所在的直线互相垂直,求∠CAB 的度数.20. 如图,在△ABC 中,记∠A=x 度,回答下列问题: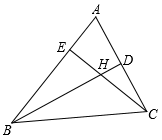 (1)、图中共有三角形个.(2)、若 BD,CE 为△ABC 的角平分线,则∠BHC=度(结果用含 x 的代数式
(1)、图中共有三角形个.(2)、若 BD,CE 为△ABC 的角平分线,则∠BHC=度(结果用含 x 的代数式表示),并证明你的结论.
(3)、若 BD,CE 为△ABC 的高线,则∠BHC=度(结果用含 x 的代数式表示),并证明你的结论.21. 已知△ABC.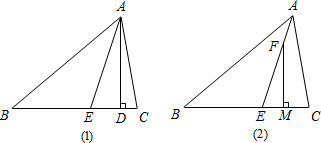 (1)、如图(1),∠C>∠B,若 AD⊥BC 于点 D,AE 平分∠BAC,你能找出∠EAD 与∠B,∠C 之间的数量关系吗?并说明理由.(2)、如图(2),AE 平分∠BAC,F 为 AE 上一点,FM⊥BC 于点 M,∠EFM 与∠B,∠C之间有何数量关系?并说明理由.
(1)、如图(1),∠C>∠B,若 AD⊥BC 于点 D,AE 平分∠BAC,你能找出∠EAD 与∠B,∠C 之间的数量关系吗?并说明理由.(2)、如图(2),AE 平分∠BAC,F 为 AE 上一点,FM⊥BC 于点 M,∠EFM 与∠B,∠C之间有何数量关系?并说明理由.