辽宁省鞍山市台安县2019-2020学年八年级上学期数学第一次月考试卷
试卷更新日期：2019-11-27 类型：月考试卷
一、单选题
-
1. 下列长度的三条线段，能组成三角形的是（ ）
A、4cm，5cm，9cm B、8cm，8cm，15cm C、5cm，5cm，10cm D、6cm，7cm，14cm2. 下列图形中，具有稳定性的是（ ）A、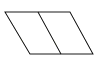
B、
C、
D、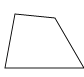
3. 在△ABC中，∠A，∠B，∠C的度数之比为2：3：4，则∠B的度数为（ ）A、120° B、80° C、60° D、40°4. 若实数m、n满足 ，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是 （ ）A、12 B、10 C、8 D、65. 如图，CE是△ABC的外角∠ACD的平分线，若∠B=35°，∠ACE=60°，则∠A=（ ）
A、95° B、75° C、35° D、85°6. 一个正n边形的每一个外角都是36°，则n=（ ）A、7 B、8 C、9 D、107. 如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（ ）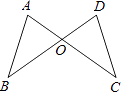
A、AB=DC B、OB=OC C、∠C=∠D D、∠AOB=∠DOC8. 如图，在△PAB中，∠A=∠B，D，E，F分别是边PA，PB，AB上的点，且AD=BF，BE=AF.若∠DFE=34°，则∠P的度数为（ ）
A、112° B、120° C、146° D、150°二、填空题
-
9. 在Rt△ABC中，∠C是直角，若∠A=30°，那么∠B=.10. 三角形三边长分别为3， ， 则a的取值范围是 ．11. 在“三角尺拼角”实验中，小明同学把一副三角尺按如图所示的方式放置，则∠1=°．
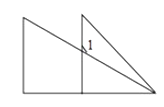12. 从一个多边形的某顶点出发，连接其余各顶点，把该多边形分成了4个三角形，则这个多边形是边形.13. 将两张三角形纸片如图摆放，量得∠1+∠2+∠3+∠4=220°，则∠5=.
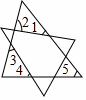14. 如图，△ABC≌△DBE，A、D、C在一条直线上，且∠A=60°，∠C=35°，则∠DBC=°.
15. 已知AD是△ABC的高，∠DAB=45°，∠DAC=34°，则∠BAC=.16. 如图，已知AB＝AC，AF＝AE，∠EAF＝∠BAC，点C、D、E、F共线.则下列结论，其中正确的是(填序号).
①△AFB≌△AEC；②BF＝CE；③∠BFC＝∠EAF；④AB＝BC.
三、解答题
-
17. 如图，已知△ABC中，DE//BC，∠AED=50°，CD是△ABC的角平分线，求∠CDE的度数.
18. 一个多边形的内角和与外角和的和恰好是十二边形的内角和，求这个多边形的边数.19. 如图，在△ABC中，∠B=100° ，按要求完成画图并解答问题：
(1)、画出△ABC的高CE，中线AF，角平分线BD，且AF所在直线交CE于点H，BD与AF相交于点G；(2)、若∠FAB=40°，求∠AFB的度数和∠BCE的度数.20. 如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)、求∠CBE的度数；(2)、过点D作DF∥BE，交AC的延长线于点F，求∠F的度数.21. 如图，点A、C在直线EF上，BC=AD，AB=CD，AE=CF.求证：∠E=∠F.
22. 如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF.能否由上面的已知条件证明AB∥ED？如果能，请给出证明；如果不能，请从下列三个条件中选择一个合适的条件，添加到已知条件中，使AB∥ED成立，并给出证明.
供选择的三个条件（请从其中选择一个）：
①AB=ED；
②BC=EF；
③∠ACB=∠DFE.
23. 如图BD、CE是△ABC的高，点P在BD的延长线上，BP=AC，点Q在CE上，CQ=AB.判断线段AP和AQ的大小、位置关系，并证明.
24. 学习几何的一个重要方法就是要学会抓住基本图形，让我们来做一次研究性学习.
(1)、如图①所示的图形，像我们常见的学习用品一圆规，我们常把这样的图形叫做“规形图”.请你观察“规形图”，试探究∠BOC与∠A、∠B、∠C之间的关系，并说明理由：(2)、如图②，若△ABC中，BO平分∠ABC，CO平分∠ACB，且它们相交于点O，试探究∠BOC与∠A的关系；(3)、如图③，若△ABC中，∠ABO= ∠ABC，∠ACO= ∠ACB，且BO、CO相交于点O，请直接写出∠BOC与∠A的关系式为_.25. 如图所示.在△ABC中，∠ACB=90°，AC=BC，过点C任作一直线PQ，过点A作 于点M，过点B作BN PQ于点N.
(1)、如图①，当M、N在△ABC的外部时，MN、AM、BN有什么关系呢？为什么？(2)、如图②，当M、N在△ABC的内部时，（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请指出MN与AM、BN之间的数关系并说明理由.