江苏省连云港市灌云县西片2019-2020学年八年级上学期数学10月月考试卷
试卷更新日期：2019-11-27 类型：月考试卷
一、单选题
-
1. 下列图形中是轴对称的是（ ）A、
B、
C、
D、
2. 如图，△ABO≌△DCO，∠D=80°，∠DOC=70°，则∠B=（ ）.
A、35° B、30° C、25° D、20°3. 如图，要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C、D，使CD＝BC，再作出BF的垂线DE，使A，C，E在一条直线上，可以说明△EDC≌△ABC最恰当的理由是（ ）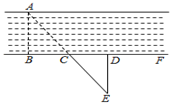
A、边角边 B、角边角 C、边边边 D、边边角4. 如图，在 正方形网格中，已将图中的四个小正方形涂上阴影，若再从图中选一个涂上阴影，使得整个阴影部分组成的图形是轴对称图形，那么不符合条件的小正方形是（ ）
A、① B、② C、③ D、④5. 如图，兔子的三个洞口A、B、C构成△ABC，猎狗想捕捉兔子，必须到三个洞口的距离都相等，则猎狗应蹲守在（ ）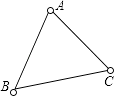
A、三条边的垂直平分线的交点 B、三个角的角平分线的交点 C、三角形三条高的交点 D、三角形三条中线的交点6. 如图，BE=CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还要添加一个条件是（ ）
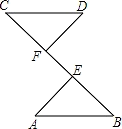A、AB=DC B、∠A=∠D C、∠B=∠C D、AE=BF7. 已知：如图，∠AOB内一点P，P1 ， P2分别P是关于OA、OB的对称点，P1P2交OA于M，交OB于N，若P1P2＝6cm，则△PMN的周长是（ ）
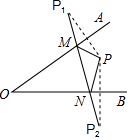A、3cm B、4cm C、5cm D、6cm8. 如图，在 和 中， ，连接 交于点 ，连接 ．下列结论：① ；② ；③ 平分 ；④ 平分 ．其中正确的个数为（ ）．
A、4 B、3 C、2 D、1二、填空题
-
9. 给出下列4种图形：①线段，②等腰三角形，③平行四边形，④圆.其中，不一定是轴对称图形的是（填写序号）.10. 如图，BF＝EC，∠A＝∠D，那么要得到△ABC≌△DEF，可以添加一个条件（只需填上一个正确的条件.
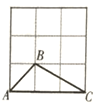
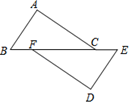11. 在如图所示的2×2方格中，连接AB、AC，则∠1+∠2=度.
12. 如果△ABC与△A'B'C'关于直线l对称，且∠A＝50°，∠B'＝70°，那么∠C'＝.13. 如图，已知 ， AD平分 于点E， ，则BC= cm。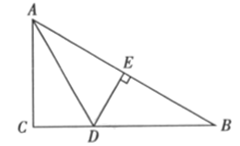
14. 如图，在△ABC中，DE是BC的垂直平分线.若AC＝8cm，△ABE的周长为13cm，则AB的长为.
15. 如图，△ABC≌△ADE，点E在BC上，若∠C＝80°，则∠DEB＝.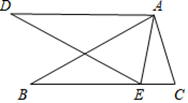
16. 如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A1 ， 称为第1次操作，折痕DE到BC的距离记为h1；还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2：按上述方法不断操作下去…，经过第2019次操作后得到的折痕D2018E2018 ， 到BC的距离记为h2019：若h1＝1，则h2019的值为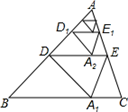
三、解答题
-
17. 如图，已知O是AB的中点，∠A＝∠B，求证：△AOC≌△BOD.
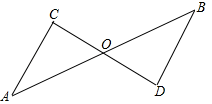18. 如图，AB＝CD，DE⊥AC，BF⊥AC，点E，F是垂足，AE＝CF，求证：
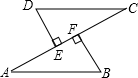(1)、△ABF≌△CDE；(2)、AB∥CD.19. 证明命题“角平分线上的点到角两边的距离相等”，要根据题意，画出图形，并用符号表示已知求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证.
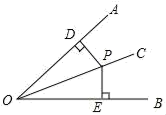(1)、已知：如图，OC是∠AOB的角平分线，点P在OC上， ， .求证：.（请你补全已知和求证）(2)、写出证明过程.20. 作图题：
(1)、在∠ABC内找一点M，使它到∠ABC的两边的距离相等，并且到点A、C的距离也相等.（写出作法，保留作图痕迹）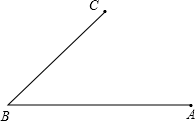
(2)、已知如下图，求作△ABC关于对称轴l的轴对称图形△AB′C′.
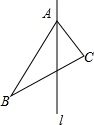21. 如图，在 的正方形网格中，有格点 和 ，且 和 关于某条直线成轴对称，请在下面给出的图中，画出3个不同位置的 及其对称轴MN.
22. 如图所示，在 中， 是 平分线， 的垂直平分线分别交 延长线于点 .求证： .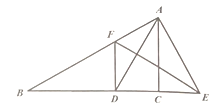
证明：∵ 平分
∴ (角平分线的定义)
∵ 垂直平分
∴ （线段垂直平分线上的点到线段两个端点距离相等）
∴ （）
∴ （等量代换）
∴ （）
23. 如图，将长方形纸片ABCD折叠，使点C与点A重合，折痕EF分别与AB、DC交于点E和点F.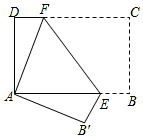
(1)、试写出图中若干相等的线段和锐角（分别写两对）；(2)、证明：△ADF≌△AB′E.24. 如图，Rt△ABC中，AB＝AC，∠BAC＝90°，直线l为经过点A的任一直线，BD⊥l于D，CE⊥l于E，若BD＞CE，试问：
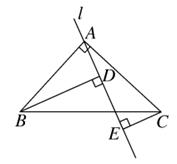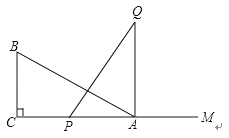
(1)、AD与CE的大小关系如何？请说明理由；(2)、线段BD，DE，CE之间的数量关系如何？请说明理由.25.如图，有一直角三角形ABC，∠C=90°，AC=10cm，BC=5cm，一条线段PQ=AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动，问P点运动到AC上什么位置时△ABC才能和△APQ全等．
26. 如图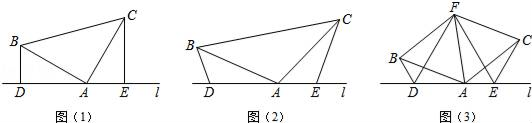
(1)、如图（1），已知：在△ABC中，∠BAC＝90°，AB＝AC，直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点D、E.证明：DE＝BD+CE.(2)、如图（2），将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线l上，且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角.请问结论DE＝BD+CE是否成立？如成立；请你给出证明；若不成立，请说明理由.(3)、拓展与应用：如图（3），D、E是直线l上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，求证：DF＝EF.