江苏省海安市八校联考2019-2020学年八年级上学期数学第一次月考试卷
试卷更新日期:2019-11-27 类型:月考试卷
一、单选题
-
1. 下列长度的三条线段能组成三角形的是( )A、5,8,14 B、3,6,11 C、4,6,10 D、2,3,42. 如果n边形的内角和是它外角和的3倍,则n等于( )A、6 B、7 C、8 D、93. 等腰三角形一个角的度数为50°,则顶角的度数为( )A、50° B、80° C、65° D、50°或80°4. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
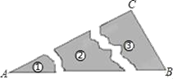 A、带①去 B、带②去 C、带③去 D、带①和②去5. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于
A、带①去 B、带②去 C、带③去 D、带①和②去5. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于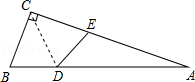 A、44° B、60° C、67° D、77°6. 如图,AD为∠BAC的平分线,添下列条件后,不能证明△ABD≌△ACD的是( )
A、44° B、60° C、67° D、77°6. 如图,AD为∠BAC的平分线,添下列条件后,不能证明△ABD≌△ACD的是( )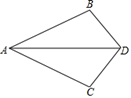 A、 B、 C、 D、7. 下列说法中,正确的是( )A、等腰三角形底边上的中线就是底边的垂直平分线 B、等腰三角形的对称轴是底边上的高 C、一条线段可看做是以它的垂直平分线为对称轴的轴对称图形 D、等腰三角形的对称轴就是顶角平分线8. 如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A、 B、 C、 D、7. 下列说法中,正确的是( )A、等腰三角形底边上的中线就是底边的垂直平分线 B、等腰三角形的对称轴是底边上的高 C、一条线段可看做是以它的垂直平分线为对称轴的轴对称图形 D、等腰三角形的对称轴就是顶角平分线8. 如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )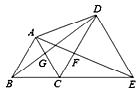 A、△ACE≌△BCD B、△BGC≌△AFC C、△DCG≌△ECF D、△ADB≌△CEA9. 如图,△ABC 中,点 D 在 BC 上,△ACD 和△ABD 面积相等,线段 AD 是三角形的( )
A、△ACE≌△BCD B、△BGC≌△AFC C、△DCG≌△ECF D、△ADB≌△CEA9. 如图,△ABC 中,点 D 在 BC 上,△ACD 和△ABD 面积相等,线段 AD 是三角形的( )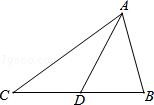 A、高 B、角平分线 C、中线 D、无法确定10. 如图,四边形 中, ,在 、 上分别找一点 ,使 周长最小时,则 的度数为( )
A、高 B、角平分线 C、中线 D、无法确定10. 如图,四边形 中, ,在 、 上分别找一点 ,使 周长最小时,则 的度数为( )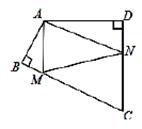 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
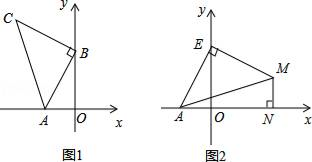
11. 点P(-2,3)关于x轴的对称点P′的坐标为.12. 一个八边形的所有内角都相等,它的每一个外角等于度.13. 如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有对.
 14. 等腰三角形的周长为20cm,一边长为6cm,则底边长为 cm.
14. 等腰三角形的周长为20cm,一边长为6cm,则底边长为 cm.
15. 如图,在一个规格为6×12(即6×12个小正方形)的球台上,有两个小球A,B.若击打小球A,经过球台边的反弹后,恰好击中小球B,那么小球A击出时,应瞄准球台边上的点.(填P1至P4点中的一个).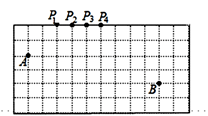 16. 如图,DE是AB的垂直平分线,AB=8,△ABC的周长是18,则△ADC的周长是 .
16. 如图,DE是AB的垂直平分线,AB=8,△ABC的周长是18,则△ADC的周长是 .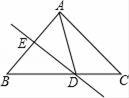 17. 如图,已知钝角三角形ABC的面积为20,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为 .
17. 如图,已知钝角三角形ABC的面积为20,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为 .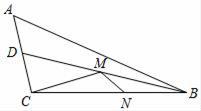
三、解答题
-
18. 已知 的三边长分别为 , , ,化简 .19. 如图,已知 各顶点的坐标分别为 .
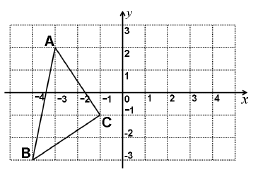
请你画出 关于 轴对称的 ,并写出 的各点坐标。
20. 如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BD=CE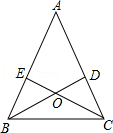 (1)、问△ABC为等腰三角形吗?为什么?(2)、问点O在∠A的平分线上吗?为什么?21. 如图,点 在 的边 上, .求证: .
(1)、问△ABC为等腰三角形吗?为什么?(2)、问点O在∠A的平分线上吗?为什么?21. 如图,点 在 的边 上, .求证: . 22. 如图,在 中, , 为 的平分线, ,垂足分别是 ,求证: .
22. 如图,在 中, , 为 的平分线, ,垂足分别是 ,求证: . 23. 如图,在 中, , 平分 ,交 于点 ,过点 作 于点 .
23. 如图,在 中, , 平分 ,交 于点 ,过点 作 于点 .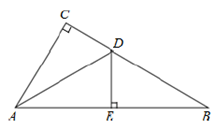 (1)、求证: ;(2)、若 ,求 的长.24. 如图,在 中, , 是 延长线上的一点,点 是 的中点。
(1)、求证: ;(2)、若 ,求 的长.24. 如图,在 中, , 是 延长线上的一点,点 是 的中点。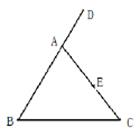 (1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
(1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。①作 的平分线 . ②连接 并延长交 于点 .
(2)、猜想与证明:试猜想 与 有怎样的关系,并说明理由。