河南省平顶山市宝丰县2019-2020学年八年级上学期数学第一次大联考试卷
试卷更新日期:2019-11-27 类型:月考试卷
一、单选题
-
1. 的相反数是( )A、5 B、0 C、 D、2. 下列数中是无理数的是( )A、 B、 C、27% D、33. 在下列长度的各组线段中,能组成直角三角形的是( )A、1,2,3 B、7,24,25 C、3,3,5 D、9,12,144. 与 最接近的正整数是( )A、2 B、3 C、4 D、55. 如图所示的是小杰使用微信告诉小宇从小宇家到小杰家的方式.根据小杰所说的,最后应向东走( )
 A、5千米 B、6千米 C、7千米 D、8千米6. 若 ,则 的立方根为( )A、-9 B、9 C、-3 D、37. 若一个直角三角形的两条直角边各扩大一倍,则其斜边( )A、不变 B、扩大一倍 C、扩大两倍 D、扩大四倍8. 如图1所示的是嘉淇爸爸给嘉淇出的一道题,如图2所示的是嘉淇对该题的解答.她所写的结论中,正确的个数是( )
A、5千米 B、6千米 C、7千米 D、8千米6. 若 ,则 的立方根为( )A、-9 B、9 C、-3 D、37. 若一个直角三角形的两条直角边各扩大一倍,则其斜边( )A、不变 B、扩大一倍 C、扩大两倍 D、扩大四倍8. 如图1所示的是嘉淇爸爸给嘉淇出的一道题,如图2所示的是嘉淇对该题的解答.她所写的结论中,正确的个数是( )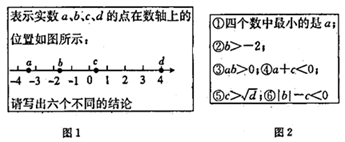 A、6 B、5 C、4 D、39. 我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )A、3平方千米 B、7.5平方千米 C、15平方千米 D、30平方千米10. 如图,由四个全等的直角三角形拼成的图形,设CE= HG= 则斜边BD的长是( )
A、6 B、5 C、4 D、39. 我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )A、3平方千米 B、7.5平方千米 C、15平方千米 D、30平方千米10. 如图,由四个全等的直角三角形拼成的图形,设CE= HG= 则斜边BD的长是( )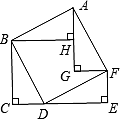 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的算术平方根是 ,﹣2的相反数是 ,的绝对值是 .12. 依据图中呈现的运算关系,可知 .
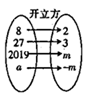 13. 某无盖圆柱形杯子的展开图如图所示,将一根长为20 的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 .
13. 某无盖圆柱形杯子的展开图如图所示,将一根长为20 的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 .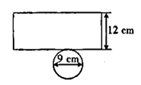 14. 观察下列等式: , , , ,…,则第8个等式是.15. 已知直角三角形的两边长分别为3和2,则这个三角形的最长边为.
14. 观察下列等式: , , , ,…,则第8个等式是.15. 已知直角三角形的两边长分别为3和2,则这个三角形的最长边为.三、解答题
-
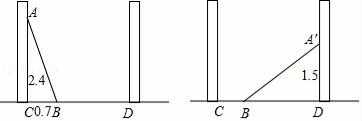
16. 计算:17. 已知一个数的平方根是 ,算术平方根是 ,且 ,求这个数.18. 如图,小巷左石两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A′D为1.5米,求小巷有多宽.
 19. 如图,在 中, 是 边上一点,连接 ,若 , , , .
19. 如图,在 中, 是 边上一点,连接 ,若 , , , .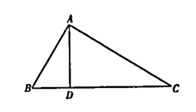 (1)、求 的度数.(2)、求 的长.20. 有个填写运算符号的游戏:在“ □ □ □ ”中的每个“口”内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.(1)、计算:(2)、若 口 请推算“口”内的运算符号.(3)、在“ □ □ □ ”的“口”内填入运算符号后,使计算所得的数最小,直接写出这个最小的数.21. 如图, ,线段 , ,一机器人 在点 处.
(1)、求 的度数.(2)、求 的长.20. 有个填写运算符号的游戏:在“ □ □ □ ”中的每个“口”内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.(1)、计算:(2)、若 口 请推算“口”内的运算符号.(3)、在“ □ □ □ ”的“口”内填入运算符号后,使计算所得的数最小,直接写出这个最小的数.21. 如图, ,线段 , ,一机器人 在点 处.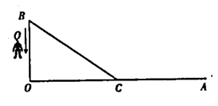 (1)、若 ,求线段 的长.(2)、在(1)的条件下,若机器人 从点 出发,以 的速度沿着 的三条边逆时针走一圈后回到点 ,设行走的时间为 ,则当 为何值时, 是以 点为直角顶点的直角三角形?22. 如图,直径为1个单位长度的圆片上有一点 与数轴上的原点重合.(所有结果均保留 )
(1)、若 ,求线段 的长.(2)、在(1)的条件下,若机器人 从点 出发,以 的速度沿着 的三条边逆时针走一圈后回到点 ,设行走的时间为 ,则当 为何值时, 是以 点为直角顶点的直角三角形?22. 如图,直径为1个单位长度的圆片上有一点 与数轴上的原点重合.(所有结果均保留 )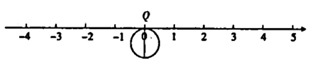 (1)、若该圆片从原点沿数轴向左滚动一周,圆片上与原点重合的点 到达点 ,设点 表示的数为 .
(1)、若该圆片从原点沿数轴向左滚动一周,圆片上与原点重合的点 到达点 ,设点 表示的数为 .①求 的值;
②求 的算术平方根.
(2)、若圆片在数轴上向右滚动的周数记为正数,向左滚动的周数记为负数,依次滚动的情况记录如下:+2,-1,+3,-4,-3.①第几次滚动后,点 距离原点最近?第几次滚动后,点 距离原点最远?
②当圆片结束运动时,点 运动的路程共有多少?此时点 所表示的数是多少?
23. 如图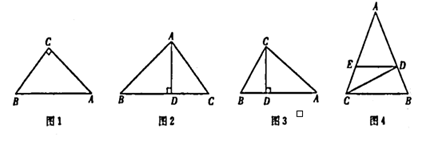 (1)、【特例感知】
(1)、【特例感知】①如图1, 为等腰直角三角形,则 (填“>“=”或“<);
②如图2, 为 的高,若 ,则 (填“>“=”或“<);
(2)、【形成概念】若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为金高三角形,两边的交点为金点.
【知识应用】
①如图3, 为金高三角形( ,其中 为金点, 是边 上的高,若 ,试求线段 的长度;
②如图4,等腰 为金高三角形,其中 , 为边 上的高,过点 作 ,与边 交于点 .若 ,试求线段 的长.