贵州省遵义市2019-2020学年八年级上学期数学10月月考试卷
试卷更新日期:2019-11-27 类型:月考试卷
一、单选题
-
1. 如图,图形中,具有稳定性的是( )A、
 B、
B、 C、
C、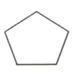 D、
D、 2. 下面四个美术字可以看作轴对称图形的是( )A、
2. 下面四个美术字可以看作轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,已知 , , ,则 的度数是( )
3. 如图,已知 , , ,则 的度数是( )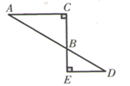 A、 B、 C、 D、4. 如图,已知 , , ,且 、 、 在同一直线上,且 , ,则 的长为( )
A、 B、 C、 D、4. 如图,已知 , , ,且 、 、 在同一直线上,且 , ,则 的长为( )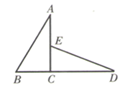 A、 B、 C、 D、不确定5. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),他哥哥说他只要带第2块去,就能配一块与原来大小一样的三角形玻璃,能得到完全一样的三角形的依据是( )
A、 B、 C、 D、不确定5. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),他哥哥说他只要带第2块去,就能配一块与原来大小一样的三角形玻璃,能得到完全一样的三角形的依据是( )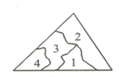 A、 B、 C、 D、6. 如下图,已知 , ,下列条件中不能判定 ≌ 的是( )
A、 B、 C、 D、6. 如下图,已知 , ,下列条件中不能判定 ≌ 的是( )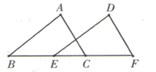 A、 B、 C、 D、7. 下列判断正确的个数是( )
A、 B、 C、 D、7. 下列判断正确的个数是( )①两个正三角形一定是全等图形;②三角形的一个外角一定大于与它不相邻的一个内角;③三角形的三条高一定交于同一点;④两边和一角对应相等的两个三角形全等.
A、3个 B、2个 C、1个 D、0个8. 一个正多边形的一个内角是它相邻的外角的3倍,则这个正多边形的边数是( )A、12 B、10 C、8 D、69. 现有长度分别是30cm和25cm的两根木棒,如果不改变木棒的长度,要将木棒首尾顺次相接钉成一个三角形木架,那么在下列长度的木棒中不能选取的是( )A、10cm的木棒 B、30cm的木棒 C、50cm的木棒 D、70cm的木棒10. 如图,点 , , 在同一直线上, 的平分线 与 边交于点 ,连接 , , , ,则 的度数是( )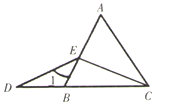 A、 B、 C、 D、11. 如图, 中, ,点 、 在 、 上,沿 向内折叠 ,得 ,则图中 的和等于( )
A、 B、 C、 D、11. 如图, 中, ,点 、 在 、 上,沿 向内折叠 ,得 ,则图中 的和等于( )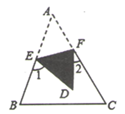 A、 B、 C、 D、12. 如图,点 是 的外角平分线上一点,且满足 ,过点 作 于点 , 交 的延长线于点 ,则下列结论:① ;② ;③ ;④ .
A、 B、 C、 D、12. 如图,点 是 的外角平分线上一点,且满足 ,过点 作 于点 , 交 的延长线于点 ,则下列结论:① ;② ;③ ;④ .其中正确的结论有( )
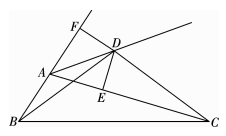 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 图中有个三角形.
 14. 如图,点 , 在线段 上, , .若要使 ≌ ,可以添加的条件是:.
14. 如图,点 , 在线段 上, , .若要使 ≌ ,可以添加的条件是:. 15. 如图所示,在 中, , , 于点 ,且 ,若点 在边 上移动,则 的最小值为.
15. 如图所示,在 中, , , 于点 ,且 ,若点 在边 上移动,则 的最小值为.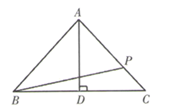
三、解答题
-
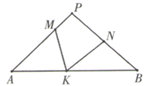
16. 如图,在 中, , 、 、 分别是 , , 上的点,且 , .若 ,则 的度数为.
 17. 计算:18. 如图, , 是 上两点,且 ;点 , , 在同一直线上, ,
17. 计算:18. 如图, , 是 上两点,且 ;点 , , 在同一直线上, ,求证: ≌ .
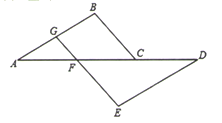 19. 已知一个等腰三角形的两边分别是不等式组 的整数解,求这个等腰三角形的周长.20. 如图,已知 的平分线 和 的平分线 相交于 , .
19. 已知一个等腰三角形的两边分别是不等式组 的整数解,求这个等腰三角形的周长.20. 如图,已知 的平分线 和 的平分线 相交于 , .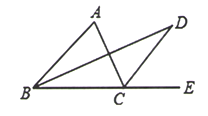 (1)、判断 与 位置关系,并说明理由;(2)、如果 ,求 的度数.21. 已知a、b、c是三角形的三边长(1)、化简: ;(2)、若 , , ,求这个三角形的周长.22. 小明站在池塘边的 点处,池塘的对面(小明的正北方向) 处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆 旁,接着再往前走了12步,到达 处,然后他改向正南方向继续行走,当小明看到电线杆 、小树 与自己现处的位置 在一条直线上时,他共走了60步.
(1)、判断 与 位置关系,并说明理由;(2)、如果 ,求 的度数.21. 已知a、b、c是三角形的三边长(1)、化简: ;(2)、若 , , ,求这个三角形的周长.22. 小明站在池塘边的 点处,池塘的对面(小明的正北方向) 处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆 旁,接着再往前走了12步,到达 处,然后他改向正南方向继续行走,当小明看到电线杆 、小树 与自己现处的位置 在一条直线上时,他共走了60步. (1)、根据题意,画出示意图(写出作图步骤);(2)、如果小明一步大约40 ,估算出小明在点 处时小树与他的距离为多少米,并说明理由.23. 如图,点 在线段 上, , , , 平分 .
(1)、根据题意,画出示意图(写出作图步骤);(2)、如果小明一步大约40 ,估算出小明在点 处时小树与他的距离为多少米,并说明理由.23. 如图,点 在线段 上, , , , 平分 .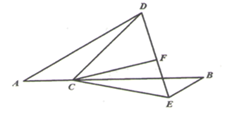 (1)、求证: ;(2)、试判断 和 的位置关系,并说明理由.24. 如图
(1)、求证: ;(2)、试判断 和 的位置关系,并说明理由.24. 如图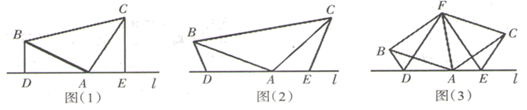 (1)、如图(1),已知:在等腰直角三角形 中, ,直线 经过点 , 直线 , 直线 ,垂足分别为点 、 .则 、 和 之间的数量关系是:.(2)、如图(2),将(1)中的条件改为:在等腰三角形 中, 、 、 三点都在直线 上,且 ,其中 为任意锐角或钝角.请问结论 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3), 、 是直线 上的两动点( 、 、 三点互不重合),点 为 平分线上的一点,且 和 均为等边三角形,连接 、 ,若 ,求证: .
(1)、如图(1),已知:在等腰直角三角形 中, ,直线 经过点 , 直线 , 直线 ,垂足分别为点 、 .则 、 和 之间的数量关系是:.(2)、如图(2),将(1)中的条件改为:在等腰三角形 中, 、 、 三点都在直线 上,且 ,其中 为任意锐角或钝角.请问结论 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3), 、 是直线 上的两动点( 、 、 三点互不重合),点 为 平分线上的一点,且 和 均为等边三角形,连接 、 ,若 ,求证: .