初中数学浙教版八年级上册5.5 一次函数的简单应用 基础巩固训练
试卷更新日期：2019-11-26 类型：同步测试
一、单选题
-
1. 气温y(℃)随高度x(km)的变化而变化的情况如下表，由表可知，气温y随着高度x的增大而（ ）
高度x/km
0
1
2
3
4
5
6
7
8
气温y/℃
28
22
16
10
4
－2
－8
－14
－20
A、升高 B、降低 C、不变 D、以上都不对2. 甲、乙两家商场平时以同样价格出售相同的商品，春节期间两家商场都让利酬宾，如图是购买甲、乙两家商场该商品的实际金额 、 （元）与原价 （元）的函数图象，下列说法正确的是（ ）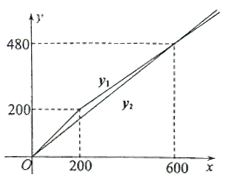
A、当 时，选甲更省钱 B、当 时，甲、乙实际金额一样 C、当 时，选乙更省钱 D、当 时，选甲更省钱3. 如图是一辆汽车行驶的速度（千米/时）与时间（分）之间变化图，下列说法正确的是（ ）
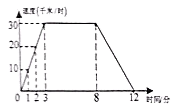A、时间是因变量，速度是自变量 B、从 分到 分，汽车行驶的路程是 千米 C、时间每增加 分钟，汽车的速度增加 千米时 D、第 分钟时汽车的速度是 千米/时4. 已知A，B两地相距3千米，小黄从A地到B地，平均速度为4千米／小时，若用x表示行走的时间(小时)，y表示余下的路程(千米)，则y关于x的函数解析式是（ ）A、y=4x(x≥0) B、y=4x-3(x≥ ) C、y=3-4x(x≥0) D、y=3-4x(0≤x≤ )5. 小涵与阿嘉一起去咖啡店购买同款咖啡豆，咖啡豆每公克的价钱固定，购买时自备容器则结帐金额再减5元.若小涵购买咖啡豆250公克且自备容器，需支付295元；阿嘉购买咖啡豆x公克但没有自备容器，需支付y元，则y与x的关系式为下列何者？（ ）
A、 B、 C、 D、6. 用100元钱在网上书店恰好可购买m本书，但是每本书需另加邮寄费6角，购买n本书共需费用y元，则可列出关系式（ ）A、 B、 C、 D、7. 某航空公司规定，旅客乘机所携带行李的运费y（元）与其质量x（kg）由（如图所示）一次函数确定，那么旅客可携带的免费行李的最大质量为（ ）
A、15kg B、20kg C、23kg D、25kg8. 已知A、B两地相距4km，上午8：00时，亮亮从A地步行到B地，8：20时芳芳从B地出发骑自行车到A地，亮亮和芳芳两人离A地的距离S（km）与亮亮所用时间t（min）之间的函数关系如图所示，芳芳到达A地时间为（ ）
A、8：30 B、8：35 C、8：40 D、8：45二、填空题
-
9. 一个三角形的底边长是24厘米，当底边上的高 （厘米）变化时，三角形的面积 也随之变化，可用式子表示 .10. 甲、乙两车从A地出发，匀速驶向B地.甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶。乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇.在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示，则m=.点H的坐标。
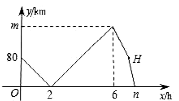
11. 某汽车生产厂对其生产的 型汽车进行油耗试验，试验中汽车为匀速行驶，在行使过程中，油箱的余油量 （升）与行驶时间 （小时）之间的关系如下表：（小时）
0
1
2
3
（升）
100
92
84
76
由表格中 与 的关系可知，当汽车行驶小时，油箱的余油量为40升.
12. 在弹性限度内，弹簧的长度y（cm）是所挂物体质量x（kg）的一次函数．一根弹簧不挂物体时长15cm；当所挂物体的质量为5kg时，弹簧长20cm．所挂物体质量为8kg时弹簧的长度是cm．三、解答题
-
13. 今年的五一小长假，两位家长计划带领若干名孩子去旅游，参加旅游的孩子人数估计为2至8名，他们联系了报价均为每人500元的两家旅行社经协商，甲旅行社的优惠条件是两位家长全额收费孩子都按七折收费；乙方旅行社的优惠条件是：家长、孩子都按八折收费．假设这两位家长带领x名孩子去旅游，他们选择哪家旅行社支付的旅游费用较少？14. 市场上甲种商品的采购价为60元/件，乙种商品的采购价为100元/件，某商店需要采购甲、乙两种商品共15件，且乙种商品的件数不少于甲种商品件数的2倍．设购买甲种商品 件（ >0），购买两种商品共花费 元．(1)、求出 与 的函数关系式（写出自变量 的取值范围）；(2)、试利用函数的性质说明，当采购多少件甲种商品时，所需要的费用最少？15. 某公司把一批货物运往外地，有两种运输方案可供选择．
方案一：使用快递公司的邮车运输，装卸收费400元，另外每千米再回收4元；
方案二：使用快递公司的火车运输，装卸收费820元，另外每千米再回收2元．
(1)、分别求邮车、火车运输总费用y1（元）、y2（元）关于运输路程x（km）之间的函数关系式：(2)、如何选择运输方案，运输总费用比较节省？