2017年湖北省宜昌市九年级四月调研数学试卷
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
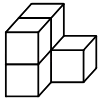
1. 下列各数中,最大的数是( )A、﹣5 B、0 C、2 D、﹣32. 用五块大小相同的小正方体搭成如图所示的几何体,这个几何体的俯视图是( )
 A、
A、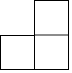 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、2×3=0 B、3﹣1=﹣3 C、x÷x=x D、(﹣a)2=a24. 计算并化简 的结果为( )A、 B、 C、4 D、165. 下列汽车标志中即是轴对称图形又是中心对称图形的是( )A、
3. 下列计算正确的是( )A、2×3=0 B、3﹣1=﹣3 C、x÷x=x D、(﹣a)2=a24. 计算并化简 的结果为( )A、 B、 C、4 D、165. 下列汽车标志中即是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,下列关系正确的是( )
6. 如图,下列关系正确的是( ) A、∠2<∠1 B、∠2>∠1 C、∠2≥∠1 D、∠2=∠17. 如图,已知菱形ABCD的周长为12,∠A=60°,则BD的长为( )
A、∠2<∠1 B、∠2>∠1 C、∠2≥∠1 D、∠2=∠17. 如图,已知菱形ABCD的周长为12,∠A=60°,则BD的长为( )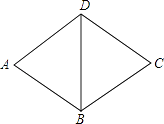 A、3 B、4 C、6 D、88. 方程 的解是( )A、x=2 B、x=﹣2 C、x=1 D、x=﹣19. 据调查,一部手机上的细菌平均可以达到600000000个,这个数字用科学记数法表示为( )A、6×10 B、600×10 C、6×108 D、0.6×1010. 某校参加校园青春健身操比赛的16名运动员的身高如表:
A、3 B、4 C、6 D、88. 方程 的解是( )A、x=2 B、x=﹣2 C、x=1 D、x=﹣19. 据调查,一部手机上的细菌平均可以达到600000000个,这个数字用科学记数法表示为( )A、6×10 B、600×10 C、6×108 D、0.6×1010. 某校参加校园青春健身操比赛的16名运动员的身高如表:身高(cm)
172
173
175
176
人数(个)
4
4
4
4
则该校16名运动员身高的平均数和中位数分别是(单位:cm)( )
A、173cm,173cm B、174cm,174cm C、173cm,174cm D、174cm,175cm11. 如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( ) A、 cm B、4cm C、3cm D、2cm12. 如图,天平右盘中的每个砝码的质量为1g,则物体M的质量m(g)的取值范围,在数轴上可表示为( )
A、 cm B、4cm C、3cm D、2cm12. 如图,天平右盘中的每个砝码的质量为1g,则物体M的质量m(g)的取值范围,在数轴上可表示为( )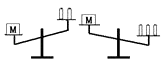 A、
A、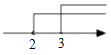 B、
B、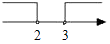 C、
C、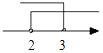 D、
D、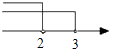 13. 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
13. 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )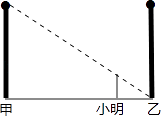 A、7米 B、8米 C、9米 D、10米14. 在一个不透明的袋中,有若干个白色乒乓球和4个黄色乒乓球,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回袋中,通过大量重复摸球实验后发现,摸到黄球的频率稳定在40%,那么,估计袋中白色乒乓球的个数为( )A、6 B、8 C、10 D、1215. 如图,函数y= 与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )A、
A、7米 B、8米 C、9米 D、10米14. 在一个不透明的袋中,有若干个白色乒乓球和4个黄色乒乓球,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回袋中,通过大量重复摸球实验后发现,摸到黄球的频率稳定在40%,那么,估计袋中白色乒乓球的个数为( )A、6 B、8 C、10 D、1215. 如图,函数y= 与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )A、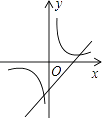 B、
B、 C、
C、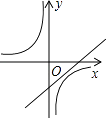 D、
D、
二、解答题
-
16. 解不等式组: .17. 先化简,再求值:( + )÷ ,其中x= ﹣1.18. 已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
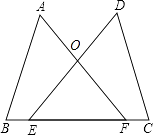 (1)、求证:AB=DC;(2)、求证:△OEF是等腰三角形.19.
(1)、求证:AB=DC;(2)、求证:△OEF是等腰三角形.19.已知,点A的坐标是(﹣1,﹣3),点B的坐标是(﹣3,﹣2),点C的坐标是(﹣3,﹣3)
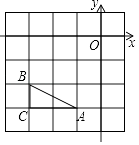 (1)、请将△ABC绕点B逆时针旋转90°,点A,C的对应点分别是点D,E,画出旋转后的△BDE,直接写出点D,E的坐标;(2)、在旋转过程中,点A所经过的路径是一段圆弧,求 的长度.20. 某数学兴趣小组对该校学生一天的零用钱数额(单位:元)进行了随机抽样调查,现将抽样数据分成五组(第一组:0~1元,含0元,1元;第二组:1元~2元,含2元;第三组:2元~3元,含3元;第四组:3元~4元,含4元;第五组:4元~5元,含5元),其统计图如图所示.第一组的人数、频率分别为2,0.04,第二、三、五组的频率分别为0.24,0.20,0.36.
(1)、请将△ABC绕点B逆时针旋转90°,点A,C的对应点分别是点D,E,画出旋转后的△BDE,直接写出点D,E的坐标;(2)、在旋转过程中,点A所经过的路径是一段圆弧,求 的长度.20. 某数学兴趣小组对该校学生一天的零用钱数额(单位:元)进行了随机抽样调查,现将抽样数据分成五组(第一组:0~1元,含0元,1元;第二组:1元~2元,含2元;第三组:2元~3元,含3元;第四组:3元~4元,含4元;第五组:4元~5元,含5元),其统计图如图所示.第一组的人数、频率分别为2,0.04,第二、三、五组的频率分别为0.24,0.20,0.36.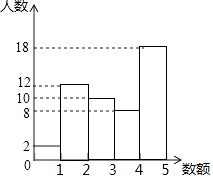 (1)、该数学兴趣小组随机抽样了多少名学生?(2)、请你通过计算后,补全统计图.(3)、如果我们在校园中随机抽查一名学生,一天的零用钱在2元以上(不含2元)的学生被抽到的概率是多少?21. 如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BC= ,AD= ,CD=12,过AB的中点E作AB的垂线交BC的延长线于F.
(1)、该数学兴趣小组随机抽样了多少名学生?(2)、请你通过计算后,补全统计图.(3)、如果我们在校园中随机抽查一名学生,一天的零用钱在2元以上(不含2元)的学生被抽到的概率是多少?21. 如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BC= ,AD= ,CD=12,过AB的中点E作AB的垂线交BC的延长线于F.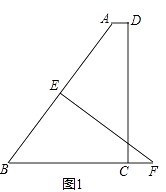 (1)、求BF的长;(2)、如图2,以点C为原点,建立平面直角坐标系,请通过计算判断,过E点的反比例函数图象与直线AB是否还有另一个交点?
(1)、求BF的长;(2)、如图2,以点C为原点,建立平面直角坐标系,请通过计算判断,过E点的反比例函数图象与直线AB是否还有另一个交点?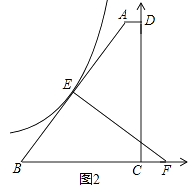 22. “WJ一号”水稻种子,当年种植,当年收割,当年出水稻产量,(以后每年要出产量还需重要新种植),某村2014、2015、2016年连续尝试种植了此水稻种子.2015年和2016年种植面积都比上年减少相同的数量,若2016年平均每公顷水稻产量比2015年增加的百分数是2015年比2014年增加的百分数的1.25倍,2016年比2014年种植面积减少的百分数与2016年水稻总产量比2014年增加的百分数相同,都等于2015年比上年平均每公顷水稻产量增加的百分数.(1)、求2016年平均每公顷水稻产量比2015年增加的百分数;(2)、求2015年这种水稻总产量比上年增加的百分数.23. 如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点.
22. “WJ一号”水稻种子,当年种植,当年收割,当年出水稻产量,(以后每年要出产量还需重要新种植),某村2014、2015、2016年连续尝试种植了此水稻种子.2015年和2016年种植面积都比上年减少相同的数量,若2016年平均每公顷水稻产量比2015年增加的百分数是2015年比2014年增加的百分数的1.25倍,2016年比2014年种植面积减少的百分数与2016年水稻总产量比2014年增加的百分数相同,都等于2015年比上年平均每公顷水稻产量增加的百分数.(1)、求2016年平均每公顷水稻产量比2015年增加的百分数;(2)、求2015年这种水稻总产量比上年增加的百分数.23. 如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点.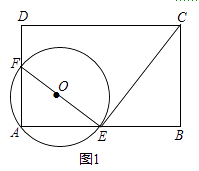 (1)、求证:圈O与CE相切与点E;(2)、如图1,若AF=2FD且∠AEF=30°,求n的值;
(1)、求证:圈O与CE相切与点E;(2)、如图1,若AF=2FD且∠AEF=30°,求n的值; (3)、如图2.若EF=EC且圈O与边CD相切,求n的值.
(3)、如图2.若EF=EC且圈O与边CD相切,求n的值.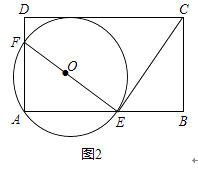 24.
24.如图,已知A(2,0),B(1,m2﹣4m+5).
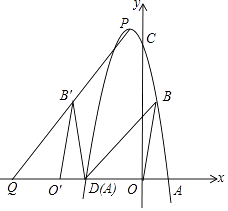 (1)、直接判断△ABO是什么图形;(2)、如果S△ABO有最小值,求m的值;(3)、抛物线y=﹣(x﹣2)(x﹣n)经过点B且与y轴交于点C,与x轴交于两点A,D.
(1)、直接判断△ABO是什么图形;(2)、如果S△ABO有最小值,求m的值;(3)、抛物线y=﹣(x﹣2)(x﹣n)经过点B且与y轴交于点C,与x轴交于两点A,D.①用含m的式子表示点C和点D坐标;
②点P是抛物线上x轴上方任一点,PQ∥BD交x轴于点Q,将△ABO向左平移到△A′B′O′,点A,B,O的对应点分别是A′,B′,O′,当点A'与点D重合时,点B'在线段PQ上,如果点P恰好是抛物线顶点,求m的值.