2017年湖北省襄阳市襄州区中考数学模拟试卷(5月份)
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
1. 2017的相反数是( )A、2017 B、﹣2017 C、 D、﹣2. 实数 的值在( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间3. 下列计算正确的是( )A、3a+4b=7ab B、(ab3)3=ab6 C、x12÷x6=x6 D、(a+2)2=a2+44. 如图,AB∥CD,射线AE交CD于点F,若∠1=125°,则∠2的度数是( )
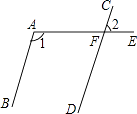 A、55° B、65° C、75° D、85°5. 2017年4月8日,中国财经新闻报道中国3月外汇储备30090.9亿,这个数据用科学记数法表示为( )A、3.00909×104 B、3.00909×105 C、3.00909×1012 D、3.00909×10136.
A、55° B、65° C、75° D、85°5. 2017年4月8日,中国财经新闻报道中国3月外汇储备30090.9亿,这个数据用科学记数法表示为( )A、3.00909×104 B、3.00909×105 C、3.00909×1012 D、3.00909×10136.如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 7. 某校九年级(1)班全体学生2017年初中毕业体育考试的成绩统计如表:
7. 某校九年级(1)班全体学生2017年初中毕业体育考试的成绩统计如表:成绩(分)
25
29
26
24
27
28
30
人数(人)
6
6
9
8
10
5
6
根据表中的信息判断,下列结论中错误的是( )
A、该班一共有50名同学 B、该班学生这次考试成绩的众数是30分 C、该班学生这次考试成绩的中位数是27分 D、该班学生这次考试成绩的平均数是26.8分8. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( ) A、8 B、10 C、12 D、149. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A、8 B、10 C、12 D、149. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( ) A、50° B、51° C、51.5° D、52.5°10. 如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
A、50° B、51° C、51.5° D、52.5°10. 如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) A、π B、π+5 C、 D、
A、π B、π+5 C、 D、二、填空题
-
11. 分解因式:m3﹣4m= .12. 已知x﹣2y=3,那么代数式3+2x﹣4y的值是 .13. 某校在甲、乙两名同学中选拔一人参加襄阳广播电台举办“国学风,少年颂”襄阳首届少年儿童经典诵读大赛.在相同的测试条件下,两人3次测试成绩(单位:分)如下:甲:79,86,82;乙:88,79,90.从甲、乙两人3次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率是 .14. 如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件使其成为菱形(只填一个即可).
 15. 若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为 .16. 如图,在正方形ABCD中,△APBC是等边三角形,连接PD,DB,则 = .
15. 若点O是等腰△ABC的外心,且∠BOC=60°,底边BC=2,则△ABC的面积为 .16. 如图,在正方形ABCD中,△APBC是等边三角形,连接PD,DB,则 = .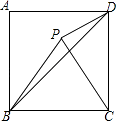
三、解答题
-
17. 化简求值:( ﹣ )÷ ,其中x= ﹣1.18. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
 (1)、这次调查的学生共有多少名?(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.(3)、如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).19. 如图,一次函数y1=kx+b(k<0)与反比例函数y2= 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))
(1)、这次调查的学生共有多少名?(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.(3)、如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).19. 如图,一次函数y1=kx+b(k<0)与反比例函数y2= 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))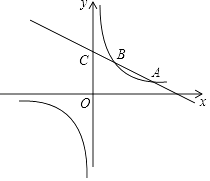 (1)、求反比例函数和一次函数的解析式;(2)、写出y1>y2时,x的取值范围.20. 某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.(1)、求购买一个甲种足球、一个乙种足球各需多少元;(2)、今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?21. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M.
(1)、求反比例函数和一次函数的解析式;(2)、写出y1>y2时,x的取值范围.20. 某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.(1)、求购买一个甲种足球、一个乙种足球各需多少元;(2)、今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?21. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M. (1)、求证:△AEC≌△ADB;(2)、若BC=2,∠BAC=30°,当四边形ADFC是菱形时,求BF的长.22. 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1)、求证:△AEC≌△ADB;(2)、若BC=2,∠BAC=30°,当四边形ADFC是菱形时,求BF的长.22. 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E. (1)、求证:AC平分∠DAB;(2)、连接CE,若CE=6,AC=8,求AE的长.23. 某淘宝店专销某种品牌的运动服,每套进价70元,售价120元/套.为了促销,淘宝店决定凡是一次购买数量不超过10套的,按原价每套120元购买;10套以上的,每多买1套,每套降价1元,每多买2套,每套降价2元……(例如,某人一次性购买15套运动服,多出5套,按每套降价5元购买,共需(15×115)元;但是最低价90元/套.(1)、求顾客一次至少买多少套,才能以最低价购买?(2)、写出当一次购买x(x>10)件时,利润w(元)与购买量x(件)之间的函数关系式;(3)、有一天,一位顾客买了35套运动服,另一位顾客买了40套运动服,淘宝店发现卖了40套反而比卖35套赚的钱少!为了使每次卖的数量多赚的钱也多,在其它促销条件不变的情况下,最低价为90元/套至少要提高到多少?为什么?24.
(1)、求证:AC平分∠DAB;(2)、连接CE,若CE=6,AC=8,求AE的长.23. 某淘宝店专销某种品牌的运动服,每套进价70元,售价120元/套.为了促销,淘宝店决定凡是一次购买数量不超过10套的,按原价每套120元购买;10套以上的,每多买1套,每套降价1元,每多买2套,每套降价2元……(例如,某人一次性购买15套运动服,多出5套,按每套降价5元购买,共需(15×115)元;但是最低价90元/套.(1)、求顾客一次至少买多少套,才能以最低价购买?(2)、写出当一次购买x(x>10)件时,利润w(元)与购买量x(件)之间的函数关系式;(3)、有一天,一位顾客买了35套运动服,另一位顾客买了40套运动服,淘宝店发现卖了40套反而比卖35套赚的钱少!为了使每次卖的数量多赚的钱也多,在其它促销条件不变的情况下,最低价为90元/套至少要提高到多少?为什么?24.如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,已知AD=8,HC:HB=3:5.
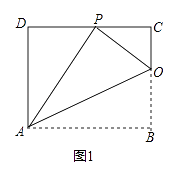 (1)、求证:△HCP∽△PDA;(2)、探究AB与HB之间的数量关系,并证明你的结论;(3)、连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.25.
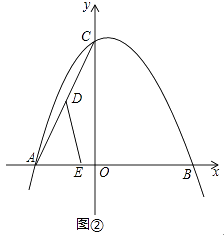
(1)、求证:△HCP∽△PDA;(2)、探究AB与HB之间的数量关系,并证明你的结论;(3)、连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.25.已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣4,0),B点坐标为(6,0),点D为AC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
 (1)、求抛物线的解析式;(2)、如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;(3)、
(1)、求抛物线的解析式;(2)、如图①,将△ADE以DE为轴翻折,点A的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;(3)、如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.