2017年湖北省襄阳市谷城县中考数学模拟试卷(5月份)
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
1. ﹣2017的倒数是( )A、2017 B、﹣2017 C、 D、﹣2. 下列计算正确的是( )A、3a+4b=7ab B、(ab3)2=ab6 C、(a+2)2=a2+4 D、x12÷x6=x63. 如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
 A、38° B、42° C、48° D、58°4. 不等式组 的解集在数轴上表示正确的是( )A、
A、38° B、42° C、48° D、58°4. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列四个实数中,最小的是( )A、 B、2 C、 D、1.46. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
5. 下列四个实数中,最小的是( )A、 B、2 C、 D、1.46. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、 B、
B、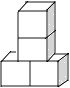 C、
C、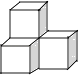 D、
D、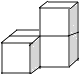 7. 某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:
7. 某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:人数(人)
1
3
4
1
分数(分)
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是( )
A、90,90 B、90,85 C、90,87.5 D、85,858. 如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( ) A、4 B、3 C、2 D、9. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是 上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )
A、4 B、3 C、2 D、9. 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是 上不与点A、点C重合的一个动点,连接AD、CD,若∠APB=80°,则∠ADC的度数是( )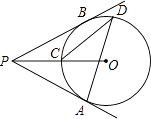 A、15° B、20° C、25° D、30°10. 在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )A、
A、15° B、20° C、25° D、30°10. 在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 我国第一艘航母“辽宁舰”最大排水量为67500吨,67500这个数用科学记数法表示这个数字是 .12. 在﹣1、3、﹣2这三个数中,任选两个数的积作为k的值,使反比例函数 的图象在第一、三象限的概率是 .13. 已知A,B两地相距160km,一辆汽车从A地到B地的速度比原来提高了25%,结果比原来提前0.4h到达,这辆汽车原来的速度是 km/h.14.
4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是米.
 15. 有一面积为5 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .16. 如图,在Rt△ABC中,∠ACB=90°,AC=2 ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 .
15. 有一面积为5 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .16. 如图,在Rt△ABC中,∠ACB=90°,AC=2 ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 .
三、解答题.
-
17. 先化简,再求值:( ﹣x﹣1)÷ ,其中x= ,y= .18. 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.若图案中三条彩条所占面积是图案面积的 ,求横、竖彩条的宽度.
 19. 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y= (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,﹣2).求:
19. 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y= (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ,点B的坐标为(m,﹣2).求: (1)、反比例函数和一次函数的解析式;(2)、写出当反比例函数的值大于一次函数的值时x的取值范围.20. “校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题:
(1)、反比例函数和一次函数的解析式;(2)、写出当反比例函数的值大于一次函数的值时x的取值范围.20. “校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题: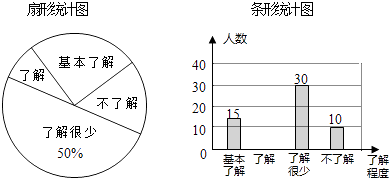 (1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21. 如图,在▱ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
(1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.21. 如图,在▱ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F. (1)、求证:AB=CF;(2)、连接DE,若AD=2AB,求证:DE⊥AF.22. 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
(1)、求证:AB=CF;(2)、连接DE,若AD=2AB,求证:DE⊥AF.22. 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC. (1)、求证:∠FBC=∠FCB;(2)、已知FA•FD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.23. 某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.(1)、求一次函数y=kx+b的表达式;(2)、若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?(3)、若该商场获得利润不低于500元,试确定销售单价x的范围.24.
(1)、求证:∠FBC=∠FCB;(2)、已知FA•FD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.23. 某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.(1)、求一次函数y=kx+b的表达式;(2)、若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?(3)、若该商场获得利润不低于500元,试确定销售单价x的范围.24.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
 (1)、
(1)、当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
 (2)、
(2)、当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.

①求证:BD⊥CF;
②当AB=2,AD=3 时,求线段DH的长.
25.如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
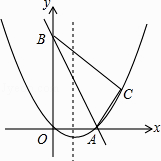 (1)、求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?(3)、在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?(3)、在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.