2017年湖北省襄阳市保康县中考数学模拟试卷(5月份)
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
1. 若|a|=2,则a的值是( )A、﹣2 B、2 C、 D、±22. 我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示为( )A、7.5×105 B、7.5×10﹣5 C、0.75×10﹣4 D、75×10﹣63. 如图,水平放置的几何体中,主视图不是长方形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、(a+b)2=a2+b2 B、a8÷a4=a2 C、2a+3b=5ab D、a2•a3=a55. 不等式组 的整数解有( )A、0个 B、5个 C、6个 D、无数个6. 若点A(﹣2,y1)、B(﹣1,y2)、C(1,y3)在反比例函数y= 的图象上,则( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y1>y3 D、y1>y3>y27.
4. 下列运算正确的是( )A、(a+b)2=a2+b2 B、a8÷a4=a2 C、2a+3b=5ab D、a2•a3=a55. 不等式组 的整数解有( )A、0个 B、5个 C、6个 D、无数个6. 若点A(﹣2,y1)、B(﹣1,y2)、C(1,y3)在反比例函数y= 的图象上,则( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y1>y3 D、y1>y3>y27.如图,在平面直角坐标系中,A(﹣3,2)、B(﹣1,0)、C(﹣1,3),将
△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1 , 点A、B、C的
对应点分别A1、B1、C1 , 则点A1的坐标为( )
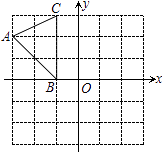 A、(3,﹣3) B、(1,﹣1) C、(3,0) D、(2,﹣1)8. 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A、(3,﹣3) B、(1,﹣1) C、(3,0) D、(2,﹣1)8. 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )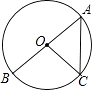 A、 π B、 π C、 π D、 π9.
A、 π B、 π C、 π D、 π9.如图,是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点,第三行有4个点,第四行有8个点,….那么这个三角点阵中前n行的点数之和可能是( )
 A、510 B、511 C、512 D、51310. 如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )
A、510 B、511 C、512 D、51310. 如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( ) A、60 B、64 C、68 D、72
A、60 B、64 C、68 D、72二、填空题
-
11. 函数 中,自变量的取值范围是 .12. 若关于x的方程 + =2的解为正数,则m的取值范围是 .13. 如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为m(结果保留根号).
 14. 已知在Rt△ABC中,∠C=90°,AB=5cm,BC=3cm,把Rt△ABC绕AB旋转一周,所得几何体的表面积是 .15. 某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2 , 该型号飞机着陆后滑行m才能停下来.
14. 已知在Rt△ABC中,∠C=90°,AB=5cm,BC=3cm,把Rt△ABC绕AB旋转一周,所得几何体的表面积是 .15. 某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2 , 该型号飞机着陆后滑行m才能停下来.三、解答题
-
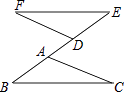
16. 先化简再求值: ,其中x=tan60°﹣1.17. 已知:如图,BC∥EF,BC=EF,AE=DB.证明:AC=DF.
 18. 八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
18. 八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
请你根据上面提供的信息回答下列问题:
(1)、扇形图中跳绳部分的扇形圆心角为度,该班共有学生人,训练后篮球定时定点投篮平均每个人的进球数是 .(2)、老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.19. 如图,已知直线y=ax+b与双曲线y= (x>0)在第一象限内交于A(x1 , y1),B(x2 , y2)两点,与x轴交于点C(x0 , 0)
(1)、若A(2,2)、B(4,n)①求直线和双曲线解析式
②直接写出S△AOB=
(2)、直接写出x1、x2、x0之间的数量关系.
20. 现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.(1)、求该快递公司投递总件数的月平均增长率;(2)、如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?21. 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,BC=6, .求BE的长.22. 中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为P= ,且其日销售量y(kg)与时间t(天)的关系如表:
(1)、求证:CD是⊙O的切线;(2)、过点B作⊙O的切线交CD的延长线于点E,BC=6, .求BE的长.22. 中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为P= ,且其日销售量y(kg)与时间t(天)的关系如表:时间t(天)
1
3
6
10
20
40
…
日销售量y(kg)
118
114
108
100
80
40
…
(1)、已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?(2)、问哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.23. 提出问题:(1)、如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
 (2)、
(2)、如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
 (3)、
(3)、在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.
 24.
24.如图,在平面直角坐标系xOy中,直线y= x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣ 且经过A、C两点,与x轴的另一交点为点B.
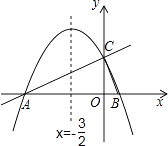 (1)、①直接写出点B的坐标;②求抛物线解析式.(2)、若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.(3)、抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、①直接写出点B的坐标;②求抛物线解析式.(2)、若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.(3)、抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.