2017年广东省深圳市龙华区中考数学二模试卷

试卷更新日期：2017-07-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 如果向东走3米记作+3 米，那么向西走2 米记作（）

A、 $\frac{1}{2}$ 米 B、 $- \frac{1}{2}$ 米 C、2 米 D、﹣2 米

查看试题解析
2. 据龙华区发展和财政局公布，2016 年1﹣12月龙华区一般公共预算支出约260 亿元，数据260 亿用科学记数法表示为（）

A、2.6×10¹⁰ B、0.26×10¹¹ C、26×10⁹ D、2.6×10⁹

查看试题解析
3. 下列运算正确的是（）

A、a²+a²=a⁴ B、（ab）²=ab² C、a⁶÷a²=a³ D、（2a²）³=8a⁶

查看试题解析
4. 下列图形均是一些科技创新公司标志图，其中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 据报道，深圳今年4 月2 日至4 月8 日每天的最高气温变化如图所示．则关于这七天的最高气温的数据，下列判断中错误的是（）

A、平均数是26 B、众数是26 C、中位数是27 D、方差是 $\frac{4}{7}$

查看试题解析
6. 已知三角形三边的长分别为1、2、x，则x的取值范围在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
7. 一个几何体由若干大小相同的小立方块搭成，图分别是从它的正面、上面看到的形状图，则搭成该几何体的小立方块至少需要（）

A、5 块 B、6 块 C、7 块 D、8 块

查看试题解析
8. 如图，已知∠MAN=55°，点B为AN上一点．用尺规按如下过程作图：
以点A为圆心，以任意长为半径作弧，交AN于点D，交AM于点E；以点B为圆心，以AD为半径作弧，交AB于点F；以点F为圆心，以DE为半径作弧，交前面的弧于点G；连接BG并延长交AM于点C．则∠BCM的度数为（）

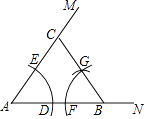A、70° B、110° C、125° D、130°

查看试题解析
9. 如图，已知五边形ABCDE 是⊙O 的内接正五边形，且⊙O 的半径为1．则图中阴影部分的面积是（）

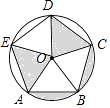A、 $\frac{1}{5} π$ B、 $\frac{2}{5} π$ C、 $\frac{1}{3} π$ D、 $\frac{5}{12} π$

查看试题解析
10. 下列命题中是真命题的是（）

A、同位角相等； B、有两边及一角分别相等的两个三角形全等； C、两组对边分别相等的四边形是平行四边形； D、垂直于半径的直线是圆的切线．

查看试题解析
11. 定义一种运算“◎”，规定x◎y=ax﹣by，其中a、b为常数，且2◎3=6，3◎2=8，则a+b的值是（）

A、2 B、﹣2 C、 $\frac{16}{3}$ D、4

查看试题解析
12. 已知函数y=ax²+bx+c（a≠0）的图象与函数y=x﹣ $\frac{3}{2}$ 的图象如图所示，则下列结论：①ab＞0；②c＞﹣ $\frac{3}{2}$ ；③a+b+c＜﹣ $\frac{1}{2}$ ；④方程ax²+（b﹣1）x+c+ $\frac{3}{2}$ =0有两个不相等的实数根．其中正确的有（）

A、4 个 B、3 个 C、2 个 D、1 个

查看试题解析

二、填空题

13. 分解因式：a²b﹣4ab²+4b³= ．

查看试题解析
14. 在 $\frac{1}{3}$ ，0， $\sqrt{2}$ ，﹣1 这四个数中随机取出两个数，则取出的两个数均为正数的概率是．

查看试题解析
15. 如图，已知函数y=kx 与函数y= $\frac{k}{x}$ 的图象交于A、B 两点，过点B作BC⊥y 轴，垂足为C，连接AC．若△ABC 的面积为2，则k 的值为．

查看试题解析
16. 如图，在平面直角坐标系中，已知矩形OABC的顶点A在x轴上，OA=4，OC=3，点D为BC边上一点，以AD为一边在与点B的同侧作正方形ADEF，连接OE．当点D在边BC上运动时，OE的长度的最小值是．

查看试题解析

三、解答题

17. 计算：|﹣ $\sqrt{3}$ |﹣（ $\sqrt{2017}$ ﹣ $\sqrt{2016}$ ）⁰﹣2cos30°+（ $\frac{1}{2}$ ）^﹣² ．

查看试题解析
18. 先化简，后求值： $\frac{1}{a - 1} + \frac{2 a - 6}{a^{2} - 9} \div \frac{2 a + 2}{a + 3}$ ，其中a=tan60°．

查看试题解析
19. 现在，共享单车已遍布深圳街头，其中较为常见的共享单车有“A．摩拜单车”、“B．小蓝单车”、“C．OFO单车”、“D．小鸣单车”、“E．凡骑绿畅”等五种类型．为了解市民使用这些共享单车的情况，某数学兴趣小组随机统计部分正在使用这些单车的市民，并将所得数据绘制出了如下两幅不完整的统计图表
（图1、图2）：
根据所给信息解答下列问题：

(1)、此次统计的人数为人；根据已知信息补全条形统计图；

(2)、在使用单车的类型扇形统计图中，使用E 型共享单车所在的扇形的圆心角为度；

(3)、据报道，深圳每天有约200余万人次使用共享单车，则其中使用E型共享单车的约有万人次．

查看试题解析
20. 如图，已知矩形ABCD 中，E、F 分别为BC、AD 上的点，将四边形ABEF 沿直线EF 折叠后，点B 落在CD 边上的点G 处，点A 的对应点为点H．再将折叠后的图形展开，连接BF、GF、BG，若BF⊥GF．

(1)、求证：△ABF≌△DFG；

(2)、已知AB=3，AD=5，求tan∠CBG 的值．

查看试题解析
21. 某电器商场销售甲、乙两种品牌空调，已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%，用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2 台．

(1)、求甲、乙两种品牌空调的进货价；

(2)、该商场拟用不超过16000 元购进甲、乙两种品牌空调共10台进行销售，其中甲种品牌空调的售价为2500元/台，乙种品牌空调的售价为3500元/台．请你帮该商场设计一种进货方案，使得在售完这10 台空调后获利最大，并求出最大利润．

查看试题解析
22. 如图，在平面直角坐标系内，已知直线l₁经过原点O 及A（2，2 $\sqrt{3}$ ）两点，将直线l₁向右平移4个单位后得到直线l₂ ，直线l₂与x 轴交于点B．

(1)、求直线l₂的函数表达式；

(2)、作∠AOB 的平分线交直线l₂于点C，连接AC．求证：四边形OACB是菱形；

(3)、设点P 是直线l₂上一点，以P 为圆心，PB 为半径作⊙P，当⊙P 与直线l₁相切时，请求出圆心P 点的坐标．

查看试题解析
23.
如图1，已知二次函数y=x²+bx+c的图象与x 轴交于A（﹣1，0）、B（3，0）两点，与y 轴交于点C，顶点为D，对称轴为直线l．

(1)、求该二次函数的表达式；

(2)、若点E 是对称轴l 右侧抛物线上一点，且S_△_ADE=2S_△_AOC ，求点E 的坐标；

(3)、
如图2，连接DC 并延长交x 轴于点F，设P 为线段BF 上一动点（不与B、F 重合），过点P 作PQ∥BD 交直线BC 于点Q，将直线PQ 绕点P 沿顺时针方向旋转45°后，所得的直线交DF 于点R，连接QR．请直接写出当△PQR 与△PFR 相似时点P 的坐标．

查看试题解析