2017年福建省宁德市古田二中中考数学模拟试卷

试卷更新日期：2017-07-19 类型：中考模拟

进入出卷网下载

一、一.选择题：

1. 如果+160元表示增加160元，那么﹣60元表示（）

A、增加100元 B、增加60元 C、减少60元 D、减少220元

查看试题解析
2. 如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于（）

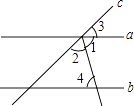A、40° B、50° C、70° D、80°

查看试题解析
3. 下列计算正确的是（）

A、a²+b³=2a⁵ B、a⁴÷a=a⁴ C、a²•a³=a⁶ D、（﹣a²）³=﹣a⁶

查看试题解析
4. 学校为了解七年级学生参加课外兴趣小组的情况，随机调查了40名学生，将结果绘制成了如图所示的统计图，则七年级学生参加绘画兴趣小组的频率是（）

A、0.1 B、0.15 C、0.25 D、0.3

查看试题解析
5. 如图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，则该几何体的主视图为（）

A、 B、 C、 D、

查看试题解析
6. 计算 $\frac{1}{x + 1} + \frac{1}{1 - x}$ 的正确结果是（）

A、0 B、 $\frac{2 x}{1 - x^{2}}$ C、 $\frac{2}{1 - x^{2}}$ D、 $\frac{2}{x^{2} - 1}$

查看试题解析
7. 一枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，投掷这样的骰子一次，向上一面点数是2或3的概率是 $\frac{a}{6}$ ，则a的值是（）

A、6 B、3 C、2 D、1

查看试题解析
8. 如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（）

A、1.8 B、2.4 C、3.2 D、3.6

查看试题解析
9. 下面所给的交通标志图中是轴对称图形的是

A、 B、 C、 D、

查看试题解析
10. 为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了A、B两类玩具，其中A类玩具的进价比B类玩具的进价每个多3元，经调查：用900元购进A类玩具的数量与用750元购进B类玩具的数量相同．设A类玩具的进价为m元/个，根据题意可列分式方程为（）

A、 $\frac{900}{m} = \frac{750}{m + 3}$ B、 $\frac{900}{m + 3} = \frac{750}{m}$ C、 $\frac{900}{m} = \frac{750}{m - 3}$ D、 $\frac{900}{m - 3} = \frac{750}{m}$

查看试题解析

二、填空题：

11. 昆明市2016年参加初中学业水平考试的人数约有67300人，将数据67300用科学记数法表示为．

查看试题解析
12. 已知（2x﹣21）（3x﹣7）﹣（3x﹣7）（x﹣13）可分解因式为（3x+a）（x+b），其中a、b均为整数，则a+3b= ．

查看试题解析
13. 近似数2.13×10³精确到位．

查看试题解析
14. 在一个不透明的口袋中，装有若干个除颜色不同外，其余都相同的小球．如果口袋中装有3个红球且从中随机摸出一个球是红球的概率为 $\frac{1}{5}$ ，那么口袋中小球共有个．

查看试题解析
15. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC．若∠CAB=22.5°，CD=8cm，则⊙O的半径为 cm．

查看试题解析
16. 如图，菱形ABCD和菱形ECGF的边长分别为2和4，∠A=120°．则阴影部分面积是．（结果保留根号）

查看试题解析

三、计算题：

17. 计算：（﹣1）²⁰¹⁶+2sin60°﹣|﹣ $\sqrt{3}$ |+π⁰ ．

查看试题解析
18. 解不等式组： ${\begin{matrix} 2 x + 1 \geq - 1 \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ ，并把不等式组的解集在数轴上表示出来．

查看试题解析
19. 如图，△ABC中，AD是高，CE是中线，点G是CE的中点，DG⊥CE，点G为垂足．

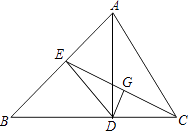(1)、求证：DC=BE；

(2)、若∠AEC=66°，求∠BCE的度数．

查看试题解析
20. 已知甲同学手中藏有三张分别标有数字 $\frac{1}{2}$ 、 $\frac{1}{4}$ 、1的卡片，乙同学手中藏有三张分别标有数字1、3、2的卡片，卡片外形相同．现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为a，b．

(1)、请你用树形图或列表法列出所有可能的结果；

(2)、现制定一个游戏规则：若所选出的a，b能使得ax²+bx+1=0有两个不相等的实数根，则甲获胜；否则乙获胜．请问这样的游戏规则公平吗？请用概率知识解释．

查看试题解析
21. 如图，△ABC是等边三角形，D、E分别是BC、AC上的点，BD=CE，求∠AFE的度数．

查看试题解析
22. 在平行四边形ABCD中，点E在AD边上，连接BE、CE，EB平分∠AEC

(1)、如图1，判断△BCE的形状，并说明理由；

(2)、如图2，若∠A=90°，BC=5，AE=1，求线段BE的长．

查看试题解析
23. 如图，在△ABC中，AB=AC，∠BAC=54°，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F．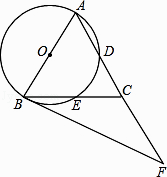

(1)、求证：BE=CE；

(2)、求∠CBF的度数；

(3)、若AB=6，求 $\hat{A D}$ 的长．

查看试题解析
24.
如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．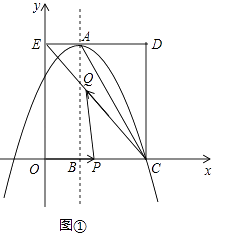

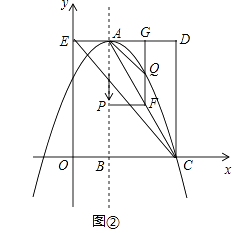
(1)、填空：点A坐标为；抛物线的解析式为．

(2)、在图①中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时，点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？

(3)、在图②中，若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？

查看试题解析
25.
在△ABC中，AB=6，AC=BC=5，将△ABC绕点A按顺时针方向旋转，得到△ADE，旋转角为α（0°＜α＜180°），点B的对应点为点D，点C的对应点为点E，连接BD，BE．

(1)、如图，当α=60°时，延长BE交AD于点F．
①求证：△ABD是等边三角形；
②求证：BF⊥AD，AF=DF；
③请直接写出BE的长；

(2)、在旋转过程中，过点D作DG垂直于直线AB，垂足为点G，连接CE，当∠DAG=∠ACB，且线段DG与线段AE无公共点时，请直接写出BE+CE的值．
温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．

查看试题解析