2017年北京市通州区中考数学二模试卷

试卷更新日期：2017-07-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 大运河森林公园位于北京市通州区的北运河两侧，占地面积约为10700亩，公园沿水系长达8公里，分别建有潞河桃柳、月岛闻莺、明镜移舟等六大景区和长虹花雨、半山人家、皇木古渡等十八处景点．将10700用科学记数法表示应为（）

A、1.07×10⁴ B、10.7×10³ C、1.07×10⁵ D、0.107×10⁵

查看试题解析
2. 实数a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最小的是（）

A、a B、b C、c D、d

查看试题解析
3. 剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
4. 如图，直线l₁ ， l₂ ， l₃交于一点，直线l₄∥l₁ ，若∠1=∠2=36°，则∠3的度数为（）

A、60° B、90° C、108° D、150°

查看试题解析
5. 如图多边形ABCDE的内角和是（）

A、360° B、540° C、720° D、900°

查看试题解析
6. 下列图形中，正方体展开后得到的图形不可能是（）

A、 B、 C、 D、

查看试题解析
7. 小明、小华两名射箭运动员在某次测试中各射箭10次，两人的平均成绩均为7.5环，如图做出了表示平均数的直线和10次射箭成绩的折线图．S₁ ， S₂分别表示小明、小华两名运动员这次测试成绩的方差，则有（）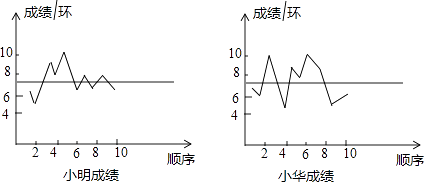

A、S₁＜S₂ B、S₁＞S₂ C、S₁=S₂ D、S₁≥S₂

查看试题解析
8. 甲、乙、丙三车从A城出发匀速前往B城．在整个行程中，汽车离开A城的距离s与时刻t的对应关系如图所示．那么8：00时，距A城最远的汽车是（）

A、甲车 B、乙车 C、丙车 D、甲车和乙车

查看试题解析
9.
如图，直线m⊥n．在平面直角坐标系xOy中，x轴∥m，y轴∥n．如果以O₁为原点，点A 的坐标为（1，1）．将点O₁平移2 $\sqrt{2}$ 个单位长度到点O₂ ，点A的位置不变，如果以O₂为原点，那么点A的坐标可能是（）

A、（3，﹣1） B、（1，﹣3） C、（﹣2，﹣1） D、（2 $\sqrt{2}$ +1，2 $\sqrt{2}$ +1）

查看试题解析
10. 甲，乙，丙三种作物，分别在山脚，山腰和山顶三个试验田进行试验，每个试验田播种二十粒种子，农业专家将每个试验田成活的种子个数统计如条形统计图，如图所示，下面有四个推断：
①甲种作物受环境影响最小；
②乙种作物平均成活率最高；
③丙种作物最适合播种在山腰；
④如果每种作物只能在一个地方播种，那么山脚，山腰和山顶分别播种甲，乙，丙三种作物能使得成活率最高．
其中合理的是（）

A、①③ B、①④ C、②③ D、②④

查看试题解析

二、填空题

11. 分解因式：a³﹣4a= ．

查看试题解析
12. 若把代数式x²﹣4x﹣5化成（x﹣m）²+k的形式，其中m，k为常数，则m+k= ．

查看试题解析
13. 2002年8月，在北京召开国际数学家大会，大会的会标取材于我国古代数学家赵爽的《勾股圆方图》．其中的“弦图”是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形，如图所示．如果直角三角形的直角边分别为a，b（a＞b），斜边为c，那么小正方形的面积可以表示为．

查看试题解析
14. 某班学生分组做抛掷同一型号的一枚图钉的实验，大量重复实验的结果统计如下表：
（顶尖朝上频率精确到 0.001）
累计实验次数
100
200
300
400
500
顶尖朝上次数
55
109
161
211
269
顶尖朝上频率
0.550
0.545
0.536
0.528
0.538
根据表格中的信息，估计掷一枚这样的图钉落地后顶尖朝上的概率为．

查看试题解析
15. 如图，Rt△ABC≌Rt△DCB，两斜边交于点O，如果AC=3，那么OD的长为．

查看试题解析
16. 阅读下面材料：
尺规作图：作一条线段等于已知线段．已知：线段AB．求作：线段CD，使CD=AB．
在数学课上，老师提出如下问题：
小亮的作法如下：
老师说：“小亮的作法正确”
请回答：小亮的作图依据是．

查看试题解析

三、解答题

17. 计算：（ $\frac{1}{2}$ ）^﹣²+（π+ $\sqrt{3}$ ）⁰﹣|2﹣ $\sqrt{3}$ |+3tan30°．

查看试题解析
18. 已知3a²+2a+1=0，求代数式2a（1﹣3a）+（3a+1）（3a﹣1）的值．

查看试题解析
19. 解方程组： ${\begin{matrix} x - y = 4 \\ 2 x + y = - 1 \end{matrix}$ ．

查看试题解析
20. 如图，在四边形ABCD中，∠A=∠B，CB=CE．求证：CE∥AD．

查看试题解析
21. 在平面直角坐标系xOy中，直线y=2x+1与双曲线y= $\frac{k}{x}$ 的一个交点为A（m，﹣3）．

(1)、求双曲线的表达式；

(2)、过动点P（n，0）（n＜0）且垂直于x轴的直线与直线y=2x+1和双曲线y= $\frac{k}{x}$ 的交点分别为B，C，当点B位于点C上方时，直接写出n的取值范围．

查看试题解析
22. 如图，在菱形ABCD中，CE垂直对角线AC于点C，AB的延长线交CE于点E．

(1)、求证：CD=BE；

(2)、如果∠E=60°，CE=m，请写出求菱形ABCD面积的思路．

查看试题解析
23. 某校组织同学到离校15千米的社会实践基地开展活动．一部分同学骑自行车前往，另一部分同学在骑自行车的同学出发 $\frac{2}{3}$ 小时后，乘汽车沿相同路线行进，结果骑自行车的与乘汽车的同学同时到达目的地．已知汽车速度是自行车速度的3倍，求自行车的速度．

查看试题解析
24. 如图，AB是⊙O的直径，PC切⊙O于点C，AB的延长线与PC交于点P，PC的延长线与AD交于点D，AC平分∠DAB．

(1)、求证：AD⊥PC；

(2)、连接BC，如果∠ABC=60°，BC=2，求线段PC的长．

查看试题解析
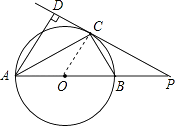25. 阅读下面材料：
当前，中国互联网产业发展迅速，互联网教育市场增长率位居全行业前列．以下是根据某媒体发布的2012﹣2015年互联网教育市场规模的相关数据，绘制的统计图表的一部分．

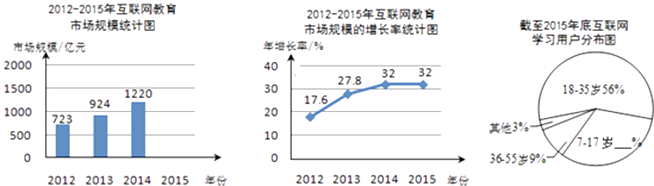(1)、2015年互联网教育市场规模约是亿元（结果精确到1亿元），并补全条形统计图；

(2)、截至2015年底，约有5亿网民使用互联网进行学习，互联网学习用户的年龄分布如图所示，请你补全扇形统计图，并估计7﹣17岁年龄段有亿网民通过互联网进行学习；

(3)、根据以上材料，写出你的思考、感受或建议（一条即可）．

查看试题解析
26. 有这样一个问题：探究函数y= $\frac{2}{x^{2}}$ ﹣ $\frac{1}{2}$ x的图象与性质．
小东根据学习函数的经验，对函数y= $\frac{2}{x^{2}}$ ﹣ $\frac{1}{2}$ x的图象与性质进行了探究．
下面是小东的探究过程，请补充完整，并解决相关问题：

(1)、函数y= $\frac{2}{x^{2}}$ ﹣ $\frac{1}{2}$ x的自变量x的取值范围是；

(2)、下表是y与x的几组对应值，求m的值；
x
…
﹣4
﹣3
﹣2
﹣ $\frac{3}{2}$
﹣1
﹣ $\frac{2}{3}$
$\frac{2}{3}$
1
2
3
4
…
y
…
   $\frac{17}{8}$
   $\frac{31}{18}$
   $\frac{3}{2}$
   $\frac{59}{36}$
   $\frac{5}{2}$
   $\frac{29}{6}$
   $\frac{25}{6}$
   $\frac{3}{2}$
﹣ $\frac{1}{2}$
﹣ $\frac{23}{18}$
m
…

(3)、如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；

(4)、进一步探究发现，该函数图象在第二象限内的最低点的坐标是（﹣2， $\frac{3}{2}$ ），结合函数的图象，写出该函数的其它性质（一条即可）．

(5)、根据函数图象估算方程 $\frac{2}{x^{2}}$ ﹣ $\frac{1}{2}$ x=2的根为．（精确到0.1）

查看试题解析
27. 已知：二次函数y=2x²+4x+m﹣1，与x轴的公共点为A，B．

(1)、如果A与B重合，求m的值；

(2)、横、纵坐标都是整数的点叫做整点；
①当m=1时，求线段AB上整点的个数；
②若设抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）整点的个数为n，当1＜n＜8时，结合函数的图象，求m的取值范围．

查看试题解析
28.
在△ABC中，AB=BC，∠ABC=90°．以AB为斜边作等腰直角三角形ADB．点P是直线DB上一个动点，连接AP，作PE⊥AP交BC所在的直线于点E．

(1)、如图1，点P在BD的延长线上，PE⊥EC，AD=1，直接写出PE的长；

(2)、点P在线段BD上（不与B，D重合），依题意，将图2补全，求证：PA=PE；

(3)、点P在DB的延长线上，依题意，将图3补全，并判断PA=PE是否仍然成立．

查看试题解析
29. 我们规定：平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d，点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D，定义点A到图形G的距离跨度为R=D﹣d．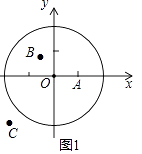

(1)、①如图1，在平面直角坐标系xOy中，图形G₁为以O为圆心，2为半径的圆，直接写出以下各点到图形G₁的距离跨度：
A（1，0）的距离跨度；
B（﹣ $\frac{1}{2}$ ， $\frac{\sqrt{3}}{2}$ ）的距离跨度；
C（﹣3，﹣2）的距离跨度；
②根据①中的结果，猜想到图形G₁的距离跨度为2的所有的点组成的图形的形状是．

(2)、如图2，在平面直角坐标系xOy中，图形G₂为以D（﹣1，0）为圆心，2为半径的圆，直线y=k（x﹣1）上存在到G₂的距离跨度为2的点，求k的取值范围．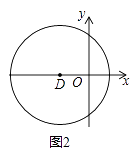

(3)、如图3，在平面直角坐标系xOy中，射线OP：y= $\frac{\sqrt{3}}{3}$ x（x≥0），⊙E是以3为半径的圆，且圆心E在x轴上运动，若射线OP上存在点到⊙E的距离跨度为2，直接写出圆心E的横坐标x_E的取值范围．

查看试题解析

累计实验次数	100	200	300	400	500
顶尖朝上次数	55	109	161	211	269
顶尖朝上频率	0.550	0.545	0.536	0.528	0.538