2017年湖北省十堰市中考数学模拟试卷
试卷更新日期：2017-07-19 类型：中考模拟
一、选择题
-
1. 在数2，1，﹣3，0中，最大的数是（ ）A、2 B、1 C、﹣3 D、02. 下列俯视图正确的是（ ）
A、
B、
C、
D、
3. 下列计算正确的是（ ）A、xy•xy=2xy B、3 ﹣ =3（x≥0） C、（2x）3=2x3 D、 • = （x≥0，y≥0）4. 如图，直线a∥直线b，若∠1=40°，∠2=75°，则∠3的大小为（ ）
A、65° B、75° C、85° D、115°5. 方程 = 的解为（ ）A、x=1 B、x=2 C、x=4 D、x=06. 某市预计2022年初中毕业生学业考试10门学科整合后的满分值如下表：科目
语文
数学
英语
理化生
政史地
体育
满分值
130
120
100
120
120
40
请问根据130，120，100，150，120，40中，众数、中位数分别是（ ）
A、150，120 B、120，120 C、130，120 D、120，1007. 如图，在平行四边形ABCD中，DE平分∠ADC，BE=2，DC=4，则平行四边形ABCD的周长为（ ）
A、16 B、24 C、20 D、128.若正整数按如图所示的规律排列，则第8行第5列的数字是（ ）
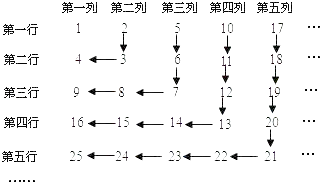A、64 B、56 C、58 D、609. 将半径为3cm的圆形纸片沿AB折叠后，圆弧恰好能经过圆心O，用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为（ ）
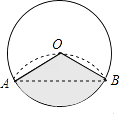A、 B、 C、 D、10. 如图，在Rt△AOB中，∠ABO=90°，点B在x轴上，点C（1，a）为OA的中点，反比例函数y= 的图象经过点C，交AB于点D，且∠AOD=∠BOD，则k=（ ）
A、8 B、2 C、 D、2二、填空题
-
11. 禽流感病毒的形状一般为球形，直径大约为0.000000102m，该直径用科学记数法表示为m．
12. 我市某果园2014年猕猴桃产量为100吨，2016年猕猴桃产量为150吨，设该果园猕猴桃产量的年平均增长率为x，则根据题意可列方程为 ．13. 如图，已知矩形ABCD中，AB=6cm，BC=8cm，E，F，G，H分别是AB，BC，CD，DA的中点，则四边形EFGH的周长等于cm．
14. 如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2 cm，∠BCD=22°30′，则⊙O的半径为cm．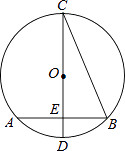
15. 一次函数y=kx+b，当1≤x≤4时，3≤y≤6，则k﹣b的值是 ．16. 如图，正方形ABCD中，AB=6，点E在边AB上，且BE=2AE．将△ADE沿ED对折至△FDE，延长EF交边BC于点G，连结DG，BF．下列结论：①△DCG≌△DFG；②BG=GC；③DG∥BF；④S△BFG=3．其中正确的结论是（填写序号）
三、解答题
-
17. 计算： ﹣2×（﹣4）﹣（﹣3）2+20170 ．18. 化简：（1﹣ ）÷（a﹣ ），然后从﹣2≤a≤2中选出一个合适的整数作为a的值代入求值．19. 如图，梯子斜靠在与地面垂直（垂足为O）的墙上，当梯子位于AB位置时，它与地面所成的角∠ABO=60°；当梯子底端向右滑动1m（即BD=1m）到达CD位置时，它与地面所成的角∠CDO=45°，求梯子的长（结果保留根号）
20. 为了解中考体育科目训练情况，某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：
(1)、本次抽样测试的学生人数是；(2)、图1中∠α的度数是 ， 并把图2条形统计图补充完整；(3)、该县九年级有学生3500名，如果全部参加这次中考体育科目测试，请估计不及格的人数为 ．(4)、测试老师想从4位同学（分别记为E、F、G、H，其中E为小明）中随机选择两位同学了解平时训练情况，请用列表或画树形图的方法求出选中小明的概率．21. 已知关于x的一元二次方程x2﹣3x+k=0有两个实数根x1和x2(1)、求实数k的取值范围；(2)、若|x1﹣x2|=3﹣x1x2时，求k的值．22. 某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=kx+b，且x=65时，y=55；x=75时，y=45．(1)、求一次函数y=kx+b的表达式；(2)、若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？23. 如图，△ABC中，∠ACB=90°，点E在BC上，以CE为直径的⊙O交AB于点F，AO∥EF
(1)、求证：AB是⊙O的切线；(2)、如图2，连结CF交AO于点G，交AE于点P，若BE=2，BF=4，求 的值．
24.将一块正方形和一块等腰直角三角形如图1摆放．
(1)、如果把图1中的△BCN绕点B逆时针旋转90°，得到图2，则∠GBM=；
(2)、将△BEF绕点B旋转．
①当M，N分别在AD，CD上（不与A，D，C重合）时，线段AM，MN，NC之间有一个不变的相等关系式，请你写出这个关系式：；（不用证明）
②当点M在AD的延长线上，点N在DC的延长线时（如图3），①中的关系式是否仍然成立？若成立，写出你的结论，并说明理由；若不成立，写出你认为成立的结论，并说明理由．
25. 已知抛物线经过点A（﹣1，0），B（3，0），C（1，4），与y轴交于点E．(1)、求抛物线的解析式(2)、点F在第三象限的抛物线上，且S△BEF=15，求点F的坐标
(3)、点P是x轴上一个动点，过P作直线l∥AE交抛物线于点Q，若以A，P，Q，E为顶点的四边形是平行四边形，请直接写出符合条件的点Q的坐标；如果没有，请通过计算说明理由．
