2017年湖北省黄石市大冶市中考数学模拟试卷(4月份)
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
1. 4的相反数是( )A、 B、﹣ C、4 D、﹣42. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 世界文化遗产长城总长约为6700000m,若将6700000用科学记数法表示为6.7×10n(n是正整数),则n的值为( )A、5 B、6 C、7 D、84. 如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )
3. 世界文化遗产长城总长约为6700000m,若将6700000用科学记数法表示为6.7×10n(n是正整数),则n的值为( )A、5 B、6 C、7 D、84. 如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )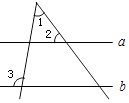 A、35° B、45° C、50° D、55°5. 下列运算正确的是( )A、x3+x2=x5 B、2x3•x2=2x6 C、(3x3)2=9x6 D、x6÷x3=x26. 下列调查方式中最适合的是( )A、要了解一批节能灯的使用寿命,采用全面调查方式 B、调查你所在班级的同学的身高,采用抽样调查方式 C、环保部门调查嘉陵江某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用全面调查方式7. 如图所示的工件的主视图是( )
A、35° B、45° C、50° D、55°5. 下列运算正确的是( )A、x3+x2=x5 B、2x3•x2=2x6 C、(3x3)2=9x6 D、x6÷x3=x26. 下列调查方式中最适合的是( )A、要了解一批节能灯的使用寿命,采用全面调查方式 B、调查你所在班级的同学的身高,采用抽样调查方式 C、环保部门调查嘉陵江某段水域的水质情况,采用抽样调查方式 D、调查全市中学生每天的就寝时间,采用全面调查方式7. 如图所示的工件的主视图是( )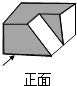 A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
8. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )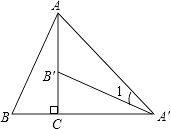 A、70° B、65° C、60° D、55°9. 如果抛物线A:y=x2﹣1通过左右平移得到抛物线B,再通过上下平移抛物线B得到抛物线C:y=x2﹣2x+2,那么抛物线B的表达式为( )A、y=x2+2 B、y=x2﹣2x﹣1 C、y=x2﹣2x D、y=x2﹣2x+110.
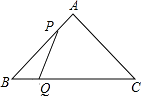
A、70° B、65° C、60° D、55°9. 如果抛物线A:y=x2﹣1通过左右平移得到抛物线B,再通过上下平移抛物线B得到抛物线C:y=x2﹣2x+2,那么抛物线B的表达式为( )A、y=x2+2 B、y=x2﹣2x﹣1 C、y=x2﹣2x D、y=x2﹣2x+110.如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 分解因式:2x2﹣18= .12. 已知关于x的一元二次方程x2﹣2x﹣k=0的一个根为﹣1,则它的另一根为 .13. 数据3,6,7,4,x的平均数是5,则这组数据的中位数是 .14. 如图,⊙O的直径AB垂直于弦CD,若∠B=30°,BC=7,则CD的长为 .
 15. 如图,Rt△ABC中,∠BCA=90°,∠BAC=30°,AB=6.△ABC以点B为中心逆时针旋转,使点C旋转至AB边延长线上的C′处,那么AC边转过的图形(图中阴影部分)的面积是 .
15. 如图,Rt△ABC中,∠BCA=90°,∠BAC=30°,AB=6.△ABC以点B为中心逆时针旋转,使点C旋转至AB边延长线上的C′处,那么AC边转过的图形(图中阴影部分)的面积是 . 16.
16.正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=x+1和x轴上,则点B6的坐标是 .

三、解答题
-
17. 计算:|2 ﹣3|﹣( )﹣1+(2017﹣ )0+4sin45°.18. 先化简,再求值:( +2﹣x)÷ ,其中x= ﹣2.19. 解不等式组 ,并把它的解集在数轴上表示出来.20. 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.求证:
 (1)、∠P=∠BAC(2)、直线CD是⊙O的切线.21. 2015年,中国女排获得第12届世界杯冠军,在女排训练中,甲、乙、丙三位队员进行战术演练,排球从一个队员随机传给另一个队员,每位传球队员传给其余两个队员的机会均等,但每位队员都不允许连续两次接触拍排球.现在要求经过两次传球(即经过一传、二传)后,第三次触球的队员再将排球扣到对方场地.(1)、若由甲开始第一次传球(即一传),经过第二次传球(即二传)后,最后排球还是由甲扣出的概率是多少?(2)、若三次触球都是随机的,求正好是甲、乙、丙分别承担一传、二传和扣球任务的概率.22.
(1)、∠P=∠BAC(2)、直线CD是⊙O的切线.21. 2015年,中国女排获得第12届世界杯冠军,在女排训练中,甲、乙、丙三位队员进行战术演练,排球从一个队员随机传给另一个队员,每位传球队员传给其余两个队员的机会均等,但每位队员都不允许连续两次接触拍排球.现在要求经过两次传球(即经过一传、二传)后,第三次触球的队员再将排球扣到对方场地.(1)、若由甲开始第一次传球(即一传),经过第二次传球(即二传)后,最后排球还是由甲扣出的概率是多少?(2)、若三次触球都是随机的,求正好是甲、乙、丙分别承担一传、二传和扣球任务的概率.22.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: ,AB=10米,AE=15米.(i=1: 是指坡面的铅直高度BH与水平宽度AH的比)
 (1)、求点B距水平面AE的高度BH;(2)、求广告牌CD的高度.
(1)、求点B距水平面AE的高度BH;(2)、求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: 1.414, 1.732)
23. 某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.时间x(天)
0
4
8
12
16
20
销量y1(万朵)
0
16
24
24
16
0
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如图所示.
 (1)、请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;(2)、观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;(3)、设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.24. 如图,△ABC中,点E、F分别在边AB,AC上,BF与CE相交于点P,且∠1=∠2= ∠A.(1)、如图1,若AB=AC,求证:BE=CF;
(1)、请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;(2)、观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;(3)、设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.24. 如图,△ABC中,点E、F分别在边AB,AC上,BF与CE相交于点P,且∠1=∠2= ∠A.(1)、如图1,若AB=AC,求证:BE=CF; (2)、若图2,若AB≠AC,
(2)、若图2,若AB≠AC,①(1)中的结论是否成立?请给出你的判断并说明理由;
②求证: = .
 25.
25.如图,反比例函数y= 的图象与一次函数y= x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
 (1)、若点P的坐标是(1,4),直接写出k的值和△PAB的面积;(2)、设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;(3)、设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
(1)、若点P的坐标是(1,4),直接写出k的值和△PAB的面积;(2)、设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;(3)、设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.