2017年河南省商丘市虞城县中考数学二模试卷
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的是( )A、﹣3 B、﹣0.2 C、0 D、|﹣4|2. “遇见最美春天”,某校组织九年级学生参观绿博园时,在植物园中了解到一种花瓣的花粉颗粒直径约为0.0000065米,0.0000065用科学记数法表示为( )A、6.5×10﹣5 B、6.5×10﹣7 C、6.5×10﹣6 D、65×10﹣63. 如图所示的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、a3+a3=a6 B、2(a+1)=2a+1 C、(a﹣b)2=a2﹣b2 D、a6÷a3=a35. 不等式组 的解集在数轴上表示为( )A、
4. 下列运算正确的是( )A、a3+a3=a6 B、2(a+1)=2a+1 C、(a﹣b)2=a2﹣b2 D、a6÷a3=a35. 不等式组 的解集在数轴上表示为( )A、 B、
B、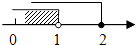 C、
C、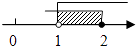 D、
D、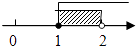 6. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )A、m≤2或m≥3 B、m≤3或m≥4 C、2<m<3 D、3<m<47. 在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( )
6. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )A、m≤2或m≥3 B、m≤3或m≥4 C、2<m<3 D、3<m<47. 在一次数学活动课上小芳,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=8,AB=30,请你帮助她算一下△ABD的面积是( ) A、150 B、130 C、240 D、1208. 小明和小亮在玩摸球游戏,在一个盒子里装有除颜色外其他均相同的2个红球和3个白球,现从中任取2个球,则取到的是一个红球,一个白球的概率为( )A、 B、 C、 D、9. 如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( )
A、150 B、130 C、240 D、1208. 小明和小亮在玩摸球游戏,在一个盒子里装有除颜色外其他均相同的2个红球和3个白球,现从中任取2个球,则取到的是一个红球,一个白球的概率为( )A、 B、 C、 D、9. 如图所示,平行四边形ABCD的对角线AC,BD交于点O,已知AD=16,BD=24,AC=12,则△OBC的周长为( ) A、26 B、34 C、40 D、5210.
A、26 B、34 C、40 D、5210.在一次数学综合实践课上,某同学将一张等边三角形纸片沿中位线剪成4个小三角形.称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是( )
 A、25 B、34 C、33 D、50
A、25 B、34 C、33 D、50二、填空题
-
11. 计算:| ﹣4|﹣( )﹣2= .12. 如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为度.
 13. 若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为 .14. 如图,在Rt△ABC中,∠ACB=90°,AC=2 ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 .
13. 若二次函数y=ax2﹣2ax+c的图象经过点(﹣1,0),则方程ax2﹣2ax+c=0的解为 .14. 如图,在Rt△ABC中,∠ACB=90°,AC=2 ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 . 15. 如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= .
15. 如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= .
三、解答题
-
16. 先化简,再求值: ÷( ﹣ ),然后从﹣ ≤x≤ 的范围内选取一个合适的整数作为x的值代入求值.17. 为了深入贯彻党的十八大精神,我省某中学为了深入学习社会主义核心价值观,特对本校部分学生(随机抽样)进行了一次相关知识的测试(成绩分为A,B,C,D,E五个组,x表示测试成绩),通过对测试成绩的分析,得到如图所示的两幅不完整的统计图,请你根据图中提供的信息解答以下问题.
A组:90≤x≤100 B组:80≤x<90 C组:70≤x<80 D组:60≤x<70 E组:x<60
 (1)、参加调查测试的学生共有人;请将两幅统计图补充完整.(2)、本次调查测试成绩的中位数落在组内.(3)、本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?18. 如图,AB是⊙O的直径,C是 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
(1)、参加调查测试的学生共有人;请将两幅统计图补充完整.(2)、本次调查测试成绩的中位数落在组内.(3)、本次调查测试成绩在80分以上(含80分)为优秀,该中学共有3000人,请估计全校测试成绩为优秀的学生有多少人?18. 如图,AB是⊙O的直径,C是 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH. (1)、求证:AC=CD;(2)、若OB=2,求BH的长.19. 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( )海里.
(1)、求证:AC=CD;(2)、若OB=2,求BH的长.19. 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( )海里. (1)、分别求出A与C及B与C的距离AC、BC(结果保留根号)(2)、已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?
(1)、分别求出A与C及B与C的距离AC、BC(结果保留根号)(2)、已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?(参考数据: =1.41, =1.73, =2.45)
20. 2016年10月20日总书记深刻指出:扶贫贵在精准,重在精准,为了贯彻落实政府提出的“精准扶贫”精神,某校特制定了一系列关于帮扶A,B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如下表:目的地
车型
A村(元/辆)
B村(元/辆)
大货车
800
900
小货车
400
600
(1)、求这15辆车中大小货车各多少辆?(2)、现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.(3)、在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.21. 如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y= (k≠0,x>0)过点D. (1)、求双曲线的解析式;(2)、作直线AC交y轴于点E,连结DE,求△CDE的面积.22. 如图①所示,已知在矩形ABCD中,AB=60cm,BC=90cm,点P从点A出发,以3cm/s的速度沿AB运动;同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).
(1)、求双曲线的解析式;(2)、作直线AC交y轴于点E,连结DE,求△CDE的面积.22. 如图①所示,已知在矩形ABCD中,AB=60cm,BC=90cm,点P从点A出发,以3cm/s的速度沿AB运动;同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s). (1)、当t=s时,△BPQ为等腰三角形;(2)、当BD平分PQ时,求t的值;(3)、如图②,将△BPQ沿PQ折叠,点B的对应点为E,PE、QE分别与AD交于点F、G.
(1)、当t=s时,△BPQ为等腰三角形;(2)、当BD平分PQ时,求t的值;(3)、如图②,将△BPQ沿PQ折叠,点B的对应点为E,PE、QE分别与AD交于点F、G.探索:是否存在实数t,使得AF=EF?如果存在,求出t的值:如果不存在,说明理由.
 23. 如图,抛物线y=﹣ x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
23. 如图,抛物线y=﹣ x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).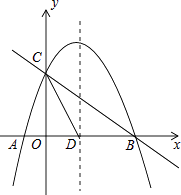 (1)、求抛物线的表达式;(2)、在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
(1)、求抛物线的表达式;(2)、在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.