2017年河南省平顶山市中考数学二模试卷
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题:
-
1. 的绝对值是( )A、 B、 C、2 D、﹣22. 使分式 有意义的x的取值范围是( )A、x≠﹣1 B、x≠1 C、x>﹣1 D、x<13. 已知关于x的方程x2+mx﹣6=0的一个根为2,则m的值及另一个根是( )A、1,3 B、﹣1,3 C、1,﹣3 D、﹣1,﹣34. 如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
 A、100° B、90° C、80° D、70°5. 为建设生态平顶山,某校学生在植树节那天,组织九年级八个班的学生到山顶公园植树,各班植树情况如下表:下列说法错误的是( )
A、100° B、90° C、80° D、70°5. 为建设生态平顶山,某校学生在植树节那天,组织九年级八个班的学生到山顶公园植树,各班植树情况如下表:下列说法错误的是( )班 级
一
二
三
四
五
六
七
八
棵 数
15
18
22
25
29
14
18
19
A、这组数据的众数是18 B、这组数据的平均数是20 C、这组数据的中位数是18.5 D、这组数据的方差为06. 如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )
7. 一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( ) A、5 B、6 C、7 D、88. 对于二次函数y=﹣ +x﹣4,下列说法正确的是( )A、当x>0时,y随x的增大而增大 B、当x=2时,y有最大值﹣3 C、图象的顶点坐标为(﹣2,﹣7) D、图象与x轴有两个交点9. 如图,AB是⊙O的直径,点F、C是⊙O上两点,且 = = ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2 ,则⊙O的半径为( )
A、5 B、6 C、7 D、88. 对于二次函数y=﹣ +x﹣4,下列说法正确的是( )A、当x>0时,y随x的增大而增大 B、当x=2时,y有最大值﹣3 C、图象的顶点坐标为(﹣2,﹣7) D、图象与x轴有两个交点9. 如图,AB是⊙O的直径,点F、C是⊙O上两点,且 = = ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2 ,则⊙O的半径为( )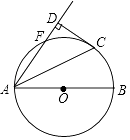 A、2 B、4 C、2 D、410.
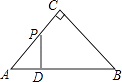
A、2 B、4 C、2 D、410.如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
 A、
A、 B、
B、 C、
C、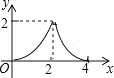 D、
D、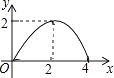
二、填空题:
-
11. (﹣1)2017﹣ = .12. 如图,点A、B是函数y= 的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积为4,则k= .
 13. 现有三张分别画有正三角形、平行四边形、菱形图案的卡片,它们除图案外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的每一张卡片的图案既是轴对称图形又是中心对称图形的概率是 .14. 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为 .
13. 现有三张分别画有正三角形、平行四边形、菱形图案的卡片,它们除图案外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽取一张,则两次抽出的每一张卡片的图案既是轴对称图形又是中心对称图形的概率是 .14. 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为 . 15. 如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是 .
15. 如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是 .
三、解答题
-
16. 判断代数式( ) 的值能否等于﹣1?并说明理由.17. 某校为了了解学生在家使用电脑的情况(分为“总是、较多、较少、不用”四种情况),随机在八、九年级各抽取相同数量的学生进行调查,绘制成部分统计图如下所示.请根据图中信息,回答下列问题:
 (1)、九年级一共抽查了名学生,图中的a= , “总是”对应的圆心角为度.(2)、根据提供的信息,补全条形统计图.(3)、若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?18. 已知函数y=2+ .(1)、写出自变量x的取值范围:;(2)、请通过列表,描点,连线画出这个函数的图象:
(1)、九年级一共抽查了名学生,图中的a= , “总是”对应的圆心角为度.(2)、根据提供的信息,补全条形统计图.(3)、若该校九年级共有900名学生,请你统计其中使用电脑情况为“较少”的学生有多少名?18. 已知函数y=2+ .(1)、写出自变量x的取值范围:;(2)、请通过列表,描点,连线画出这个函数的图象:①列表:
x
…
﹣8
﹣4
﹣3
﹣2
﹣1
﹣
1
2
3
4
8
…
y
…
1
0
﹣2
﹣6
10
6
4
3
…
②描点(在下面给出的直角坐标系中补全表中对应的各点);
③连线(将图中描出的各点用平滑的曲线连接起来,得到函数的图象).
 (3)、观察函数的图象,回答下列问题:
(3)、观察函数的图象,回答下列问题:①图象与x轴有个交点,所以对应的方程2+ =0实数根是;
②函数图象的对称性是 .
A、既是轴对称图形,又是中心对称图形
B、只是轴对称图形,不是中心对称图形
C、不是轴对称图形,而是中心对称图形
D、既不是轴对称图形也不是中心对称图形
(4)、写出函数y=2+ 与y= 的图象之间有什么关系?(从形状和位置方面说明)19. 如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).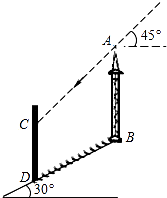 20. 如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
20. 如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C. (1)、求证:△EFB≌△ADE;(2)、当点A在⊙O上移动时,直接回答四边形FCDE的最大面积为多少.21. 小张前往某精密仪器产应聘,公司承诺工资待遇如下.进厂后小张发现:加工1件A型零件和3件B型零件需5小时;加工2件A型零件和5件B型零件需9小时.
(1)、求证:△EFB≌△ADE;(2)、当点A在⊙O上移动时,直接回答四边形FCDE的最大面积为多少.21. 小张前往某精密仪器产应聘,公司承诺工资待遇如下.进厂后小张发现:加工1件A型零件和3件B型零件需5小时;加工2件A型零件和5件B型零件需9小时.工资待遇:每月工资至少3000元,每天工作8小时,每月工作25天,加工1件A型零件计酬16元,加工1件B型零件计酬12元,月工资=底薪(800元)+计件工资.
(1)、小张加工1件A型零件和1件B型零件各需要多少小时?(2)、若公司规定:小张每月必须加工A、B两种型号的零件,且加工B型的数量不大于A型零件数量的2倍,设小张每月加工A型零件a件,工资总额为W元,请你运用所学知识判断该公司颁布执行此规定后是否违背了工资待遇承诺?22. 已知,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的上边作正方形ADEF,连接CF.(1)、观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: .
 (2)、
(2)、数学思考:如图2,当点D在线段CB的延长线上时,以上①②关系是否成立,请在后面的横线上写出正确的结论.①BC与CF的位置关系为:;②BC、CD、CF之间的数量关系为: .
 (3)、
(3)、如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GD,若已知AB=2 ,CD= BC,请求出DG的长(写出求解过程).
 23.
23.如图,在平面直角坐标系中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),C(3,1)抛物线y= x2+bx﹣2的图象过C点,交y轴于点D.

(1)、在后面的横线上直接写出点D的坐标及b的值: , b=;
(2)、平移该抛物线的对称轴所在直线l,设l与x轴交于点G(x,0),当OG等于多少时,恰好将△ABC的面积分为相等的两部分?(3)、点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,直接写出P点坐标;若不存在,说明理由.