2017年河北省唐山市路北区中考数学一模试卷
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
1. (﹣2)0的值为( )A、﹣2 B、0 C、1 D、2
-
2. (﹣2)×3的结果是( )A、﹣5 B、1 C、﹣6 D、6
-
3. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间
-
4. 把分式方程 转化为一元一次方程时,方程两边需同乘以( )A、x B、2x C、x+4 D、x(x+4)
-
5. + 的运算结果正确的是( )A、 B、 C、 D、a+b
-
6.
如图,∠1=∠2,∠3=40°,则∠4等于( )
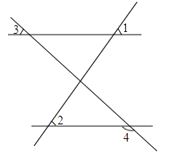 A、120° B、130° C、140° D、40°
A、120° B、130° C、140° D、40° -
7. 下列一元二次方程没有实数根的是( )A、x2+2x+1=0 B、x2+x+2=0 C、x2﹣1=0 D、x2﹣2x﹣1=0
-
8. 如图,数轴上表示的是某一不等式组的解集,则这个不等式组可能是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 自来水公司为了解居民某月用水请款个,随机抽取了20户居民的月用水量x(单位:立方米),绘制出表格,则月用水量x<3的频率是( )
月用水量
频数
0≤x<0.5
1
0.5≤x<1
2
1≤x<1.5
3
1.5≤x<2
4
2≤x<2.5
3
2.5≤x<3
3
3≤x<3.5
2
3.5≤x<4
1
4≤x<4.5
1
A、0.15 B、0.3 C、0.8 D、0.9 -
10. 如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )
 A、∠1<∠2 B、∠1>∠2 C、∠3<∠4 D、∠3>∠4
A、∠1<∠2 B、∠1>∠2 C、∠3<∠4 D、∠3>∠4 -
11. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
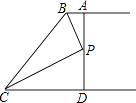 A、8 B、6 C、4 D、2
A、8 B、6 C、4 D、2 -
12. 如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求
对于两人的作法,下列判断何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确 -
13. 如图,坐标平面上有A(0,a)、B(﹣9,0)、C(10,0)点,其中a>0,若∠BAC=100°,则△ABC的外心在( )
 A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、第一象限 B、第二象限 C、第三象限 D、第四象限 -
14. 如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为何?( )
 A、10 B、11 C、 D、
A、10 B、11 C、 D、 -
15.
在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为( )
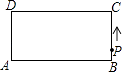 A、
A、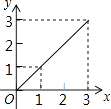 B、
B、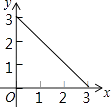 C、
C、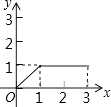 D、
D、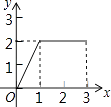
二、填空题
-
16. 据报道,2015年某市城镇非私营单位就业人员年平均工资超过60500元,将数60500用科学记数法表示为 .
-
17. 甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小明打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小明抽出的两颗求颜色相同的概率为 .
-
18. 如图,已知点A(0,2)、B(2 ,2)、C(0,4),过点C向右做平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在左侧作等边△APQ,连接PB、BA.
 (1)、当AB∥PQ时,点P的横坐标是;(2)、当BP∥QA时,点P的横坐标是 .
(1)、当AB∥PQ时,点P的横坐标是;(2)、当BP∥QA时,点P的横坐标是 .
三、解答题
-
19. 先化简,再求值: ,其中x满足方程:x2+x﹣6=0.
-
20. 国家环保局统一规定,空气质量分为5级:1级质量为优;2级质量为良;3级质量为轻度污染;4级质量为中度污染;5级质量为重度污染.某城市随机抽取了一年中某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
 (1)、本次调查共抽取了天的空气质量检测结果进行统计;(2)、补全条形统计图;(3)、扇形统计图中3级空气质量所对应的圆心角为°;(4)、如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计该年该城市只有多少天适宜户外活动.(一年天数按365天计)
(1)、本次调查共抽取了天的空气质量检测结果进行统计;(2)、补全条形统计图;(3)、扇形统计图中3级空气质量所对应的圆心角为°;(4)、如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计该年该城市只有多少天适宜户外活动.(一年天数按365天计) -
21. 如图,已知边长为6的等边△ABC内接于⊙O.
 (1)、求⊙O半径;(2)、求 的长和弓形BC的面积.
(1)、求⊙O半径;(2)、求 的长和弓形BC的面积. -
22. 如图,已知一次函数y1=kx+b的图象与反比例函数y2= 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2= 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
 (1)、求m的值;(2)、求一次函数的表达式;(3)、根据图象,当y1<y2<0时,写出x的取值范围.
(1)、求m的值;(2)、求一次函数的表达式;(3)、根据图象,当y1<y2<0时,写出x的取值范围. -
23. 如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.
 (1)、延长MP交CN于点E(如图2).
(1)、延长MP交CN于点E(如图2).①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)、若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; (3)、若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
(3)、若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由. -
24. 某高新企业员工的工资由基础工资、绩效工资和工龄工资三部分组成,其中工龄工资的制定充分了考虑员工对企业发展的贡献,同时提高员工的积极性,控制员工的流动率,对具有中职以上学历员工制定如下的工龄工资方案.
Ⅰ.工龄工资分为社会工龄工资和企业工龄工资;
Ⅱ.社会工龄=参加本企业工作时年龄﹣18,企业工龄=现年年龄﹣参加本企业工作时年龄.
Ⅲ.当年工作时间计入当年工龄
Ⅳ.社会工龄工资y1(元/月)与社会工龄x(年)之间的函数关系式如①图所示,企业工龄工资y2(元/月)与企业工龄x(年)之间的函数关系如图②所示.
请解决以下问题
 (1)、求出y1、y2与工龄x之间的函数关系式;(2)、现年28岁的高级技工小张从18岁起一直实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?(3)、已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元?
(1)、求出y1、y2与工龄x之间的函数关系式;(2)、现年28岁的高级技工小张从18岁起一直实行同样工龄工资制度的外地某企业工作,为了方便照顾老人与小孩,今年小张回乡应聘到该企业,试计算第一年工龄工资每月下降多少元?(3)、已经在该企业工作超过3年的李工程师今年48岁,试求出他的工资最高每月多少元? -
25.
如图,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M、N以每秒1个单位的速度分别从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒时,过点N作NP⊥BC,交OB于点P,连接MP.
 (1)、点B的坐标为;用含t的式子表示点P的坐标为;(2)、记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值?(3)、试探究:在上述运动过程中,是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC的 ?若存在,求出点T的坐标;若不存在,请说明理由.
(1)、点B的坐标为;用含t的式子表示点P的坐标为;(2)、记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值?(3)、试探究:在上述运动过程中,是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC的 ?若存在,求出点T的坐标;若不存在,请说明理由.
