2017年河北省唐山市古冶区中考数学一模试卷
试卷更新日期:2017-07-19 类型:中考模拟
一、选择题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、 D、2. 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 实数a、b在数轴上的对应的位置如图所示,则正确的结论是( )
3. 实数a、b在数轴上的对应的位置如图所示,则正确的结论是( ) A、b>﹣1 B、b<﹣2 C、a>﹣b D、a<﹣b4. 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
A、b>﹣1 B、b<﹣2 C、a>﹣b D、a<﹣b4. 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )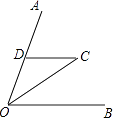 A、20° B、35° C、45° D、70°5. 下列多项式中,在实数范围内能进行因式分解的是( )A、a﹣1 B、a2﹣1 C、x2﹣4y D、a2+16. 如果a+b= ,那么代数式 =( )A、2 B、﹣2 C、 D、﹣7. 关于x的一元二次方程x2+ax﹣1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根8. 一个多边形的每个内角均为120°,则这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形9. 如图,⊙O是△ABC的外接圆,⊙O的半径为2,∠A=30°,则BC=( )
A、20° B、35° C、45° D、70°5. 下列多项式中,在实数范围内能进行因式分解的是( )A、a﹣1 B、a2﹣1 C、x2﹣4y D、a2+16. 如果a+b= ,那么代数式 =( )A、2 B、﹣2 C、 D、﹣7. 关于x的一元二次方程x2+ax﹣1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根8. 一个多边形的每个内角均为120°,则这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形9. 如图,⊙O是△ABC的外接圆,⊙O的半径为2,∠A=30°,则BC=( )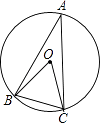 A、 B、2 C、2 D、10. 如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )
A、 B、2 C、2 D、10. 如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )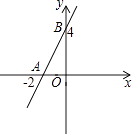 A、
A、 B、
B、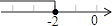 C、
C、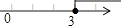 D、
D、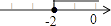 11. 某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
11. 某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )动时间(小时)
3
3.5
4
4.5
人数
1
1
2
1
A、中位数是4,平均数是3.75 B、众数是4,平均数是3.75 C、中位数是4,平均数是3.8 D、众数是2,平均数是3.812. 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=6,那么点B与C′的距离为( )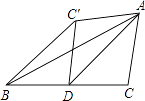 A、3 B、3 C、3 D、613. 下列说法正确的是( )A、“蒙上眼睛射击正中靶心”是必然事件 B、“抛一枚硬币,正面朝上的概率为 ”说明掷一枚质地均匀的硬币10次,必有5次正面朝上 C、“抛一枚均匀的正方体骰子,朝上的点数是3的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在 附近 D、为了解某种节能灯的使用寿命,应选择全面调查14. 烟花厂为雁荡山旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣ t2+20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )A、3s B、4s C、5s D、6s15. 如图,在已知的△ABC中,按以下步骤作图:
A、3 B、3 C、3 D、613. 下列说法正确的是( )A、“蒙上眼睛射击正中靶心”是必然事件 B、“抛一枚硬币,正面朝上的概率为 ”说明掷一枚质地均匀的硬币10次,必有5次正面朝上 C、“抛一枚均匀的正方体骰子,朝上的点数是3的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数是3”这一事件发生的频率稳定在 附近 D、为了解某种节能灯的使用寿命,应选择全面调查14. 烟花厂为雁荡山旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣ t2+20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )A、3s B、4s C、5s D、6s15. 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
 A、50° B、45° C、30° D、25°16. 如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )
A、50° B、45° C、30° D、25°16. 如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的均匀速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )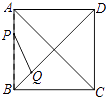 A、
A、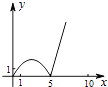 B、
B、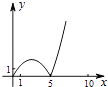 C、
C、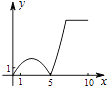 D、
D、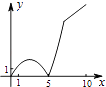
二、填空题
-
17. 方程x2﹣2x=0的根是 .18. 在实数范围内定义一种新运算“⊕”,其运算规则为:a⊕b=﹣2ab,如:1⊕5=﹣2×1×5=﹣10,则式子 ⊕ = .19. 如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤裁剪和拼图.

第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,BD= , 对角线MN长度的最小值为 .
三、解答题
-
20. 计算: +(tan60﹣1)0+| ﹣1|﹣2cos30°.21. 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
 22. 如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱,标有5,6,7的三个球放入乙箱中.
22. 如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱,标有5,6,7的三个球放入乙箱中.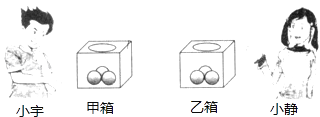 (1)、小宇从甲箱中随机摸出一个球,则“摸出标有数字是5的球”的概率是;(2)、小宇从甲箱中,小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字小于1,则称小宇“屡胜一筹”,请你用列表法(或画树状图),求小宇“屡胜一筹”的概率.23. 如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1B1C1 , AB与A1C1相交于点D,A1C1、BC1与AC分别交于点E、F.
(1)、小宇从甲箱中随机摸出一个球,则“摸出标有数字是5的球”的概率是;(2)、小宇从甲箱中,小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字小于1,则称小宇“屡胜一筹”,请你用列表法(或画树状图),求小宇“屡胜一筹”的概率.23. 如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1B1C1 , AB与A1C1相交于点D,A1C1、BC1与AC分别交于点E、F.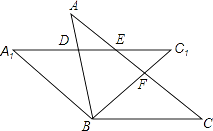 (1)、求证:△BCF≌△BA1D;(2)、当∠C=40°时,请你证明四边形A1BCE是菱形.24. 某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
(1)、求证:△BCF≌△BA1D;(2)、当∠C=40°时,请你证明四边形A1BCE是菱形.24. 某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:月产销量y(个)
…
160
200
240
300
…
每个玩具的固定成本Q(元)
…
60
48
40
32
…
(1)、每月产销量y(个)与销售单价x(元)之间的函数关系式为;从上表可知,每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;
(2)、若每个玩具的固定成本为30元,求它的销售单价是多少元?(3)、若该厂这种玩具的月产销量不超过400个,求此时销售单价最低为多少元?25. 在平面上,Rt△ABC与直径为CE的半圆O,如图1摆放,∠B=90°,BC=m,AC=2CE=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转,且∠ECD=∠ACB,旋转角记为α(0°≤α≤180°).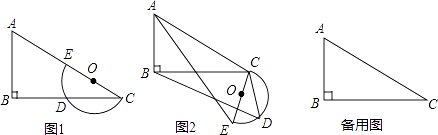 (1)、①当α=0°时,连接DE,则∠CDE=°,CD=;②当α=180°时, = .(2)、试判断:旋转过程中 的大小有无变化?请仅就图2的情形给出证明.(3)、若m=4,n=5,当α=∠ACB时,线段BD= .(4)、若m=4 ,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= .26. 如图,已知抛物线y=﹣x2+9的顶点为A,曲线DE是双曲线y= (3≤x≤12)的一部分,记作G1 , 且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2 .
(1)、①当α=0°时,连接DE,则∠CDE=°,CD=;②当α=180°时, = .(2)、试判断:旋转过程中 的大小有无变化?请仅就图2的情形给出证明.(3)、若m=4,n=5,当α=∠ACB时,线段BD= .(4)、若m=4 ,n=6,当半圆O旋转至与△ABC的边相切时,线段BD= .26. 如图,已知抛物线y=﹣x2+9的顶点为A,曲线DE是双曲线y= (3≤x≤12)的一部分,记作G1 , 且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2 .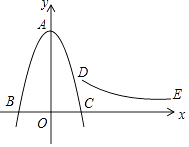 (1)、求双曲线的解析式;(2)、设抛物线y=﹣x2+9与x轴的交点为B、C,且B在C的左侧,则线段BD的长为;(3)、点(6,n)为G1与G2的交点坐标,求a的值.(4)、解:在移动过程中,若G1与G2有两个交点,设G2的对称轴分别交线段DE和G1于M、N两点,若MN< ,直接写出a的取值范围.
(1)、求双曲线的解析式;(2)、设抛物线y=﹣x2+9与x轴的交点为B、C,且B在C的左侧,则线段BD的长为;(3)、点(6,n)为G1与G2的交点坐标,求a的值.(4)、解:在移动过程中,若G1与G2有两个交点,设G2的对称轴分别交线段DE和G1于M、N两点,若MN< ,直接写出a的取值范围.