浙江省金华市义乌市七校联考2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2019-11-22 类型：期中考试

进入出卷网下载

一、单选题

1. －4的绝对值是（）

A、4 B、 $\frac{1}{4}$ C、－4 D、 $- \frac{1}{4}$

查看试题解析
2. 下列各数中，比-2小的数是（）

A、-1 B、 $- \sqrt{5}$ C、0 D、1

查看试题解析
3. 2019年“五一”期间，某景点接待海内外游客共688000人次，688000这个数用科学记数法表示为（）

A、68.8×10⁴ B、0.688×10⁶ C、6.88×10⁵ D、6.88×10⁶

查看试题解析
4. 以下各数中， $\sqrt{5} 、 \frac{22}{7} 、 - 1.732, 、 \sqrt{25} 、 \frac{π}{2} 、 3 + \sqrt{29}$ 、0.1010010001…（相邻两个1之间0的个数逐次加1），无理数的个数有（）

A、3 B、4 C、5 D、6

查看试题解析
5. 如图，在数轴上有a、b两个数，则下列结论错误的是（）.

A、a+b ＜ 0 B、a-b ＞ 0 C、a×b ＜ 0 D、 $（ - \frac{a}{b} ）^{3} < 0$

查看试题解析
6. 实数 $1 - 2 a$ 有平方根，则 $a$ 可以取的值为（）

A、 $\frac{1}{2}$ B、1 C、 $\sqrt{2}$ D、π

查看试题解析
7. 由四舍五入得到的近似数3.50万，精确到（）.

A、十分位 B、百位 C、十位 D、百分位

查看试题解析
8. 在下列结论中，正确的是（）.

A、 $\sqrt{（ - \frac{5}{4} ）^{2}} = \pm \frac{5}{4}$ B、x²的算术平方根是x C、平方根是它本身的数为0，±1 D、 $\sqrt{64}$ 的立方根是2

查看试题解析

9. 一家健身俱乐部收费标准为180元/次，若购买会员年卡，可享受如下优惠：

会员年卡类型	办卡费用（元）	每次收费（元
A类	1500	100
B类	3000	60
C类	4000	40

例如，购买A类会员年卡，一年内健身20次，消费1500+100×20=3500元.若一年内在该健身俱乐部健身的次数介于50-60次之间，则最省钱的方式为（）

A、购买C类会员年卡 B、购买B类会员年卡 C、购买A类会员年卡 D、不购买会员年卡

查看试题解析

10. 某校利用二维码进行学生学号统一编排.黑色小正方形表示1，白色小正方形表示0，将每一行数字从左到右依次记为a，b，c，d，那么利用公式 $a \times 2^{3} + b \times 2^{2} + c \times 2^{1} + d$ 计算出每一行的数据.第一行表示年级，第二行表示班级，第三行表示班级学号的十位数，第四行表示班级学号的个位数.如图1所示，第一行数字从左往右依次是1，0，0，1，则表示的数据为1×2³+0×2²+0×2¹+1=9，记作09，第二行数字从左往右依次是1，0，1，0，则表示的数据为1×2³+0×2²+1×2¹=10，记作10，以此类推，图1代表的统一学号为091034，表示9年级10班34号.小明所对应的二维码如图2所示，则他的统一学号为（）.

A、060729 B、070629 C、070627 D、060727

查看试题解析

二、填空题

11. -1 $\frac{2}{3}$ 的倒数是.

查看试题解析
12. 试举一例，说明“两个无理数的和仍是无理数”是错误的：

查看试题解析
13. 对于两个不相等的实数a，b，定义一种新的运算： $a * b = \frac{\sqrt{a + b}}{a - b}$ ，例如： $3 * 2 = \frac{\sqrt{3 + 2}}{3 - 2} = \sqrt{5}$ ，那么15*（6*3）=.

查看试题解析
14. 若a、b为实数，且 $|a + 1|$ 与 $\sqrt{b-2}$ 互为相反数，则 $（ a + b ）^{2019}$ =

查看试题解析
15. 按照下图所示的操作步骤，若输出y的值为22，则输入的值x为．

查看试题解析
16. 如图所示，在由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案中，第5个图形中阴影小三角形的个数是，第n个图形中阴影小三角形的个数是.

查看试题解析

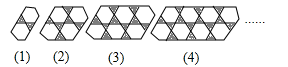
三、解答题

17. 把符合条件的数填在相应的大括号内.
-2，π，-|+0.8|， $\sqrt[3]{9}$ ，0， $- \frac{11}{7}$

整数{ …}；无理数{ …}.

查看试题解析
18. 在数轴上表示下列各数，并把这些数按从小到大的顺序用“＜”连接.
-（-1.5），3， $- \sqrt{2.25}$ ，|- 4|

查看试题解析
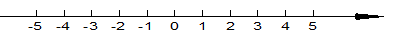19. 计算题

(1)、-5-（-19）

(2)、﹣1⁴×（﹣7）+6÷（-2）

(3)、 $（ - 36 ） \times （ \frac{1}{12} + \frac{5}{9} - \frac{7}{18} ）$

(4)、 $\sqrt{1.44} + \sqrt[3]{- 8} - \sqrt{（ - \frac{6}{5} ）^{2}}$

查看试题解析

20. 某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产为正，减产为负）：

星期	一	二	三	四	五	六	日
增减	+5	-2	-4	+13	-10	+8	-9

(1)、根据记录可知前三天共生产辆；

(2)、该厂实行计件工资制，每辆车60元，若超额完成任务，则超额的每辆奖15元，若未完成任务，则少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？

查看试题解析

21. 如图，这是由8个同样大小的立方体组成的魔方，体积为64.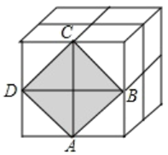

(1)、这个魔方的棱长为.

(2)、图中阴影部分是一个正方形 $A B C D$ ，求出阴影部分的面积及其边长.

(3)、把正方形 $A B C D$ 放到数轴上，如图，使得点 $A$ 与 $- 1$ 重合，那么点 $D$ 在数轴上表示的数为.

查看试题解析
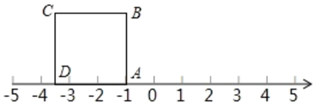22. 已知5a+2的立方根是3，3a+b-1的算术平方根是4，c是 $\sqrt{11}$ 的整数部分.

(1)、求a，b，c的值；

(2)、求3a-b+c的平方根.

查看试题解析
23. 有依次排列的3个数：4，9，7，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在两个数之间，可产生一个新数串①：4，5，9，-2，7，这称作第一次操作；对数串①进行同样的操作后也可产生一个新的数串②：4，1，5，4，9，-11，-2，9，7……依次操作下去.

(1)、数串①的所有数之和为，数串②的所有数之和为.

(2)、第3次操作以后所产生的数串③为4，， 1，4，5，， 4，5，9，-20，-11，9，-2，11，9，-2，7. 所有数之和为.

(3)、请列式计算：操作第100次产生的新数串的所有数字之和是多少？

查看试题解析
24. 如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A ， B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

(1)、数轴上点B表示的数是，点P表示的数是（用含t的代数式表示）；

(2)、动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发．求：
①当点P运动多少秒时，点P与点Q相遇？

②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？

查看试题解析