广西壮族自治区南宁市马山县2020届九年级上学期数学期中考试试卷

试卷更新日期：2019-11-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列汽车标志中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程x²=x的解是（）

A、x=0 B、x=1 C、x=0， x= 1 D、x=0 ， x=-1

查看试题解析
3. 抛物线y＝2(x+1)²－5的顶点坐标是（）

A、(1，－5) B、(－1，－5) C、(－1，－4) D、(－2，－7)

查看试题解析
4. 如图，已知△AOB是正三角形，OC⊥OB，OC=OB，将△OAB绕点O按逆时针方向旋转，使得OA与OC重合，得到△OCD，则旋转的角度是（）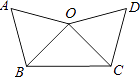

A、150° B、120° C、90° D、60°

查看试题解析
5. 关于x的一元二次方程kx²-2x-1=0有实数根，则k的取值范围是（）

A、k>-1或k≠0 B、k≥-1 C、k≤-1或k≠0 D、k≥-1且k≠0

查看试题解析
6. 将抛物线 $y = {(x - 1)}^{2} + 3$ 向左平移1个单位，再向下平移3个单位后所得抛物线的解析式为（）

A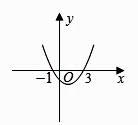、 $y = {(x - 2)}^{2}$ B、 $y = {(x - 2)}^{2} + 6$ C、 $y = x^{2} + 6$ D、 $y = x^{2}$

查看试题解析
7. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如下图，当 $y < 0$ 时， $x$ 的取值范围是（）

A、 $- 1 < x < 3$ B、 $x > 3$ C、 $x < - 1$ D、 $x > 3$ 或 $x < - 1$

查看试题解析
8. 已知二次函数y＝ $\frac{1}{3}$ (x－4)²－3的部分图象如图所示，图象再次与x轴相交时的坐标是（）

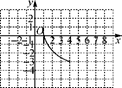A、(5，0) B、(6，0) C、(7，0) D、(8，0)

查看试题解析
9. 如图，点O是▱ABCD的对称中心，EF是过点O的任意一条直线，它将平行四边形分成两部分，四边形ABFE和四边形EFCD的面积分别记为S₁ ， S₂ ，那么S₁ ， S₂之间的关系为（）

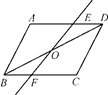A、S₁>S₂ B、S₁＜S₂ C、S₁＝S₂ D、无法确定

查看试题解析
10. 方程 $x^{2} + 6 x - 5 = 0$ 的左边配成完全平方后所得方程为（）

A、 ${(x + 3)}^{2} = 14$ B、 ${(x - 3)}^{2} = 14$ C、 ${(x + 6)}^{2} = 12$ D、以上答案都不对

查看试题解析
11. 在一次同学聚会上，每人都向其他人赠送了一份小礼品，共互送110份小礼品，如果参加聚会的同学有x名.根据题意列出的方程是（）。

A、x (x + 1) = 110 B、x (x －1) = 110 C、2x ( x + 1) = 110 D、x (x－1) = 110×2

查看试题解析
12. 已知二次函数y＝ax²＋bx＋c的图象如图所示，有以下结论：①abc＞0；②a－b＋c＜0；③2a＝b；④4a＋2b＋c＞0；⑤若点(－2，y₁)和(－ $\frac{1}{3}$ ，y₂)在该图象上，则y₁＞y₂. 其中正确的结论个数是（）

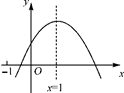A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 方程x²＋2x－3＝0的两个根分别是x₁＝， x₂＝

查看试题解析
14. 把一个正五边形绕着它的中心旋转，至少旋转度，才能与原来的图形重合.

查看试题解析
15. 三角形的两边长分别为3和6，第三边的长是方程x²﹣6x+8=0的解，则此三角形周长是．

查看试题解析
16. 若二次函数y＝x²+2x+m的图象与坐标轴有3个交点，则m的取值范围是.

查看试题解析
17. 若点A（3﹣m，2）在函数y=2x﹣3的图象上，则点A关于原点对称的点的坐标是.

查看试题解析
18. 已知（﹣1，y₁），（﹣3，y₂），（ $\frac{1}{2}$ ，y₃）在函数y＝3x²+6x+12的图象上，则y₁ ， y₂和y₃的大小关系为

查看试题解析

三、解答题

19. 解下列方程。

(1)、x²-5x+6=0

(2)、(2x＋1)(x－4)＝5.

查看试题解析
20. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：

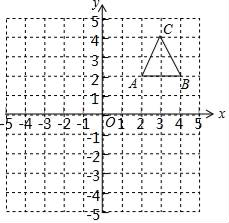
①画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出A₁的坐标．

②画出△ABC绕点B逆时针旋转90°后得到的△A₂B₂C₂ ，并写出A₂的坐标．

③画出△A₂B₂C₂关于原点O成中心对称的△A₃B₃C₃ ，并写出A₃的坐标．

查看试题解析
21. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B'C，连接AA'，若∠1= 20°，求∠B的度数.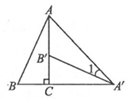

查看试题解析
22. 随着港珠澳大桥的顺利开通，预计大陆赴港澳旅游的人数将会从2018年的100万人增至2020年的144万人，求2018年至2020年这两年的赴港旅游人数的年平均增长率．

查看试题解析
23. 已知：如图，二次函数 $y = {ax}^{2} + bx + c$ 的图象与x轴交于A、B两点，其中A点坐标为 $(- 1 ， 0)$ ，点 $C (0 ， 5)$ ，另抛物线经过点 $(1 ， 8)$ ，M为它的顶点.

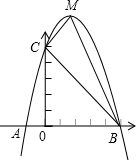(1)、求抛物线的解析式；

(2)、求 $△ MCB$ 的面积 $S_{△ MCB}$ .

查看试题解析
24. 如图，学校准备在教学楼后面搭建一个简易矩形自行车车棚，一边利用教学楼的后墙(可利用的墙长为19 m)，另外三边利用学校现有总长38 m的铁栏围成.

(1)、若围成的面积为180 m² ，试求出自行车车棚的长和宽；

(2)、能围成面积为200 m²的自行车车棚吗？如果能，请你给出设计方，如果不能，请说明理由.

查看试题解析
25. 某商品交易会上，一商人将每件进价为5元的纪念品，按每件9元出售，每天可售出32件.他想采用提高售价的办法来增加利润，经试验，发现这种纪念品每件提价1元，每天的销售量会减少4件.

(1)、当售价定为多少元时，每天的利润为140元？

(2)、商人为了获得最大利润，应将该商品每件售价定为多少元？最大利润是多少元

查看试题解析
26. 如图，抛物线y＝ax²+bx﹣4a经过A（﹣1，0），C（0，4）两点，与x轴交于另一点B.

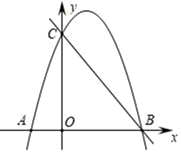(1)、求抛物线的解析式；

(2)、直接写出二次函数的函数值y＞0时，自变量x的取值范围；

(3)、已知点D（m，m+1）在第一象限的抛物线上，求点D关于直线BC对称的点的坐标.

查看试题解析