湖北省荆州市松滋市2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-11-22 类型:期中考试
一、单选题
-
1. 在下图中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为( )A、40° B、100° C、40°或100° D、70°或50°3. 在平面直角坐标系中,点P(3,5)关于 轴对称的点的坐标是( )A、(3,5) B、(3,-5) C、(-3,5) D、(-3,-5)4. 如图,在△ABC 中,∠BAC=72°,∠C=36°,∠BAC 的平分线 AD 交 BC 于 D, 则图中有等腰三角形( )
2. 已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为( )A、40° B、100° C、40°或100° D、70°或50°3. 在平面直角坐标系中,点P(3,5)关于 轴对称的点的坐标是( )A、(3,5) B、(3,-5) C、(-3,5) D、(-3,-5)4. 如图,在△ABC 中,∠BAC=72°,∠C=36°,∠BAC 的平分线 AD 交 BC 于 D, 则图中有等腰三角形( ) A、0 个 B、1 个 C、2 个 D、3 个5. 如图,在△ABC中,BC的垂直平分线分别交AC , BC于点D , E . 若△ABC的周长为22,BE=4,则△ABD的周长为( )
A、0 个 B、1 个 C、2 个 D、3 个5. 如图,在△ABC中,BC的垂直平分线分别交AC , BC于点D , E . 若△ABC的周长为22,BE=4,则△ABD的周长为( )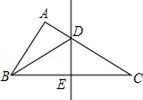 A、14 B、18 C、20 D、266. 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
A、14 B、18 C、20 D、266. 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( ) A、40° B、80° C、90° D、140°7. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A、40° B、80° C、90° D、140°7. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )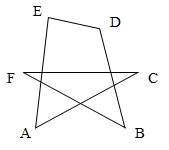 A、180° B、270° C、360° D、720°8. 已知如图:△ABC中,AB=AC , BE=CD , BD=CF , 则∠EDF=( )
A、180° B、270° C、360° D、720°8. 已知如图:△ABC中,AB=AC , BE=CD , BD=CF , 则∠EDF=( ) A、2∠A B、90°﹣2∠A C、90°﹣∠A D、90°﹣ ∠A9. 如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A、2∠A B、90°﹣2∠A C、90°﹣∠A D、90°﹣ ∠A9. 如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )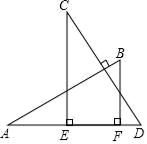 A、a+c B、b+c C、a﹣b+c D、a+b﹣c10. 如图所示,三角形ABC的面积为1cm2 . AP垂直∠B的平分线BP于P.则与三角形PBC的面积相等的长方形是( )
A、a+c B、b+c C、a﹣b+c D、a+b﹣c10. 如图所示,三角形ABC的面积为1cm2 . AP垂直∠B的平分线BP于P.则与三角形PBC的面积相等的长方形是( ) A、
A、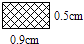 B、
B、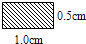 C、
C、 D、
D、
二、填空题
-
11. 若点A(m+2,3)与点B(﹣4,n+5)关于y轴对称,则m+n=12. 如果等腰三角形的两边长分别是4、8,那么它的周长是 .13. 如图,已知点A(a,b),0是原点,OA=OA1 , OA⊥OA1 , 则点A1的坐标是 .
 14. 已知△ABC的三边分别是6,8,10,△DEF的三边分别是6,6x-4,4x+2,若两个三角形全等,则x的值为.15. 如图,在 中,CM平分 交AB于点M,过点M作 交AC于点N,且MN平分 ,若 ,则BC的长为.
14. 已知△ABC的三边分别是6,8,10,△DEF的三边分别是6,6x-4,4x+2,若两个三角形全等,则x的值为.15. 如图,在 中,CM平分 交AB于点M,过点M作 交AC于点N,且MN平分 ,若 ,则BC的长为.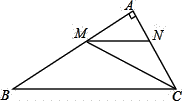 16. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于 MN的长半径画弧,两弧交于点P,作射线AP,交边BC于点D,若CD=4,AB=15,则△ABD的面积是.
16. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于 MN的长半径画弧,两弧交于点P,作射线AP,交边BC于点D,若CD=4,AB=15,则△ABD的面积是.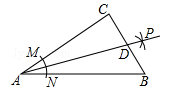
三、解答题
-
17. 如图,在钝角△ABC中.
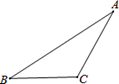 (1)、作钝角△ABC的高AM,CN;(2)、若CN=3,AM=6,求BC与AB之比.18. 如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你分别在甲、乙、丙三个图中涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形.
(1)、作钝角△ABC的高AM,CN;(2)、若CN=3,AM=6,求BC与AB之比.18. 如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你分别在甲、乙、丙三个图中涂黑一个小三角形,使它与阴影部分合起来所构成的图形是一个轴对称图形. 19. 如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AB=FD,证明△ABC≌△FDE.
19. 如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AB=FD,证明△ABC≌△FDE. 20. 如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的角平分线.
20. 如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的角平分线. (1)、若∠C=70°,∠BAC=60°,则∠BED的度数是;若∠BED=50°,则∠C的度数是.(2)、探究∠BED与∠C的数量关系,并证明你的结论.21. “综合与实践”学习活动准备制作一组三角形,记这些三角形分别为 ,用记号 表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.(1)、若这些三角形三边的长度为大于0且小于3的整数个单位长度,请用记号写出所有满足条件的三角形;(2)、如图, 是 的中线,线段 的长度分别为2个,6个单位长度,且线段 的长度为整数个单位长度,过点 作 交 的延长线于点 .
(1)、若∠C=70°,∠BAC=60°,则∠BED的度数是;若∠BED=50°,则∠C的度数是.(2)、探究∠BED与∠C的数量关系,并证明你的结论.21. “综合与实践”学习活动准备制作一组三角形,记这些三角形分别为 ,用记号 表示一个满足条件的三角形,如(2,4,4)表示边长分别为2,4,4个单位长度的一个三角形.(1)、若这些三角形三边的长度为大于0且小于3的整数个单位长度,请用记号写出所有满足条件的三角形;(2)、如图, 是 的中线,线段 的长度分别为2个,6个单位长度,且线段 的长度为整数个单位长度,过点 作 交 的延长线于点 .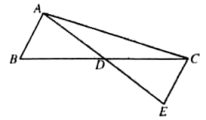
①求 的长度;
②请直接用记号表示 .
22. 如图,△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,与AB相交于点E,连接CE. (1)、证明:AE=CE=BE;(2)、若DA⊥AB,BC=6,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时PB+PC的值.23. 已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.
(1)、证明:AE=CE=BE;(2)、若DA⊥AB,BC=6,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时PB+PC的值.23. 已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.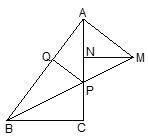
求证:
(1)、△APM是等腰三角形;(2)、PC=AN.24. 已知,在平面直角坐标系中,A(m,0)、B(0,n),m、n满足(m-n)2+|m- |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E. (1)、求∠OAB的度数;(2)、设AB=4,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;(3)、设AB=4,若∠OPD=45°,求点D的坐标.
(1)、求∠OAB的度数;(2)、设AB=4,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;(3)、设AB=4,若∠OPD=45°,求点D的坐标.