2017年海南省三亚市中考数学最后冲刺试卷（二）（6月份）
试卷更新日期：2017-07-18 类型：中考模拟
一、选择题
-
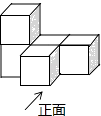
1. ﹣8的绝对值等于（ ）A、8 B、﹣8 C、 D、2. 下列运算中，正确的是（ ）A、x3+x3=x6 B、x3•x9=x27 C、（x2）3=x5 D、x÷x2=x﹣13. 若a=2，b=﹣1，则a+2b+3的值为（ ）A、﹣1 B、3 C、6 D、54. 一组数据8，3，8，6，7，8，7的众数和中位数分别是（ ）A、8，6 B、7，6 C、7，8 D、8，75. 如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是（ ）
A、
B、
C、
D、
6. 据报道，目前我国“天河二号”超级计算机的运算速度位居全球第一，其运算速度达到了每秒338600000亿次，数学338600000用科学记数法可表示为（ ）A、3.386×109 B、0.3386×109 C、33.86×107 D、3.386×1087. 实数a，b在数轴上的对应点的位置如图所示，把﹣a，﹣b，0按照从小到大的顺序排列，正确的是（ ）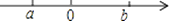
A、﹣a＜0＜﹣b B、0＜﹣a＜﹣b C、﹣b＜0＜﹣a D、0＜﹣b＜﹣a8. 某校九年级共有1、2、3、4四个班，现从这四个班中随机抽取两个班进行一场篮球比赛，则恰好抽到1班和2班的概率是（ ）A、 B、 C、 D、9. 方程 =3的解是（ ）A、﹣ B、 C、﹣4 D、410. 若点A（﹣5，y1），B（﹣3，y2），C（2，y3）在反比例函数y= 的图象上，则y1 ， y2 ， y3的大小关系是（ ）A、y1＜y3＜y2 B、y1＜y2＜y3 C、y3＜y2＜y1 D、y2＜y1＜y311. 如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一条直线上，则三角板ABC旋转的角度是（ ）
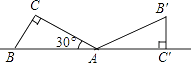A、60° B、90° C、120° D、150°12. 如图，在平行线a，b之间放置一块直角三角板，三角板的顶点A，B分别在直线a，b上，则∠1+∠2的值为（ ）
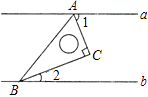A、90° B、85° C、80° D、60°13. 如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，⊙O的半径为5cm，则圆心O到弦CD的距离为（ ）
A、 cm B、3cm C、3 cm D、6cm14.如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（ ）
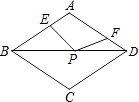A、1 B、2 C、3 D、4二、填空题
-
15. 因式分解：a3﹣ab2= ．16. 端午节期间，“惠民超市”销售的粽子打8折后卖a元，则粽子的原价卖元．17. 如图，在▱ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B=52°，∠DAE=20°，则∠FED′的大小为 ．
18. 如图，已知⊙O的半径为6，弦AB的长为8，P是AB延长线上一点，BP=2，则tan∠OPA的值是 ．
三、解答题
-
19. 计算题(1)、计算：（﹣1）2017﹣（2﹣ ）0+ ；(2)、化简：（x﹣y）2﹣（x﹣2y）（x+y）．20. 二孩政策的落实引起了全社会的关注，某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度，在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查，调查分别为非常赞同、赞同、无所谓、不赞同等四种态度，现将调查统计结果制成了如图两幅统计图，请结合两幅统计图，回答下列问题：
(1)、在这次问卷调查中一共抽取了名学生，a=%；(2)、请补全条形统计图；(3)、持“不赞同”态度的学生人数的百分比所占扇形的圆心角为度；(4)、若该校有3000名学生，请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和．21. 某商店购买60件A商品和30件B商品共用了1080元，购买50件A商品和20件B商品共用了880元．A、B两种商品的单价分别是多少元？22.为了维护海洋权益，新组建的国家海洋局加大了在南海的巡逻力度，一天，我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻，同时发现一艘不明国籍的船只停在C处海域．如图所示，AB=60（ ）海里，在B处测得C在北偏东45°的方向上，A处测得C在北偏西30°的方向上，在海岸线AB上有一灯塔D，测得AD=120（ ）海里．
(1)、分别求出A与C及B与C的距离AC、BC（结果保留根号）(2)、已知在灯塔D周围100海里范围内有暗礁群，我在A处海监船沿AC前往C处盘查，图中有无触礁的危险？（参考数据： =1.41， =1.73， =2.45）
23.如图，将矩形ABCD沿线段AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．
(1)、求证：△AGE≌△AGD(2)、探究线段EG、GF、AF之间的数量关系，并说明理由；(3)、若AG=6，EG=2 ，求BE的长．24.如图，已知点A的坐标为（﹣2，0），直线y=﹣ x+3与x轴、y轴分别交于点B和点C，连接AC，顶点为D的抛物线y=ax2+bx+c过A、B、C三点．
(1)、请直接写出B、C两点的坐标，抛物线的解析式及顶点D的坐标；(2)、设抛物线的对称轴DE交线段BC于点E，P是第一象限内抛物线上一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标；(3)、设点M是线段BC上的一动点，过点M作MN∥AB，交AC于点N，点Q从点B出发，以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒），当t（秒）为何值时，存在△QMN为等腰直角三角形？