2017年贵州省黔南州都匀市中考数学二模试卷
试卷更新日期:2017-07-18 类型:中考模拟
一、选择题
-
1. ﹣|﹣2|的倒数是( )A、2 B、 C、 D、﹣22. 下列图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件是必然事件的为( )A、购买一张彩票,中奖 B、通常加热到100℃时,水沸腾 C、任意画一个三角形,其内角和是360° D、射击运动员射击一次,命中靶心4. 下列运算正确的是( )A、﹣2x2y•3xy2=﹣6x2y2 B、(﹣x﹣2y)(x+2y)=x2﹣4y2 C、6x3y2÷2x2y=3xy D、(4x3y2)2=16x9y45. 如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=110°,则∠2等于( )
3. 下列事件是必然事件的为( )A、购买一张彩票,中奖 B、通常加热到100℃时,水沸腾 C、任意画一个三角形,其内角和是360° D、射击运动员射击一次,命中靶心4. 下列运算正确的是( )A、﹣2x2y•3xy2=﹣6x2y2 B、(﹣x﹣2y)(x+2y)=x2﹣4y2 C、6x3y2÷2x2y=3xy D、(4x3y2)2=16x9y45. 如图,已知a、b、c、d四条直线,a∥b,c∥d,∠1=110°,则∠2等于( ) A、50° B、70° C、90° D、110°6. 某校举行“中国梦•我的梦”演讲比赛,需要在初三年级选取一名主持人,共有12名同学报名参加,其中初三(1)班有2名,初三(2)班有4名,初三(3)班有6名,现从这12名同学中随机选取一名主持人,则选中的这名同学恰好是初三(1)班同学的概率是( )A、 B、 C、 D、7. 某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同.设2,3月份利润的月增长率为x,那么x满足的方程为( )A、10(1+x)2=36.4 B、10+10(1+x)2=36.4 C、10+10(1+x)+10(1+2x)=36.4 D、10+10(1+x)+10(1+x)2=36.48. 三棱柱的三视图如图所示,△EFG中,EF=6cm,∠EFG=45°,则AB的长为( )
A、50° B、70° C、90° D、110°6. 某校举行“中国梦•我的梦”演讲比赛,需要在初三年级选取一名主持人,共有12名同学报名参加,其中初三(1)班有2名,初三(2)班有4名,初三(3)班有6名,现从这12名同学中随机选取一名主持人,则选中的这名同学恰好是初三(1)班同学的概率是( )A、 B、 C、 D、7. 某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同.设2,3月份利润的月增长率为x,那么x满足的方程为( )A、10(1+x)2=36.4 B、10+10(1+x)2=36.4 C、10+10(1+x)+10(1+2x)=36.4 D、10+10(1+x)+10(1+x)2=36.48. 三棱柱的三视图如图所示,△EFG中,EF=6cm,∠EFG=45°,则AB的长为( ) A、6cm B、3 cm C、3cm D、6 cm9. 如图,直线l经过第一、二、四象限,l的解析式是y=(m﹣3)x+m+2,则m的取值范围在数轴上表示为( )
A、6cm B、3 cm C、3cm D、6 cm9. 如图,直线l经过第一、二、四象限,l的解析式是y=(m﹣3)x+m+2,则m的取值范围在数轴上表示为( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于( )
10. 如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于( ) A、40°,80° B、50°,100° C、50°,80° D、40°,100°11. 如图,用相同的小正方形按照某种规律进行摆放,则第8个图形中小正方形的个数是( )
A、40°,80° B、50°,100° C、50°,80° D、40°,100°11. 如图,用相同的小正方形按照某种规律进行摆放,则第8个图形中小正方形的个数是( ) A、71 B、78 C、85 D、8912. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A、71 B、78 C、85 D、8912. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) A、c>﹣1 B、b>0 C、2a+b≠0 D、9a+c>3b13. 如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A、c>﹣1 B、b>0 C、2a+b≠0 D、9a+c>3b13. 如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )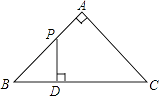 A、
A、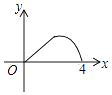 B、
B、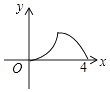 C、
C、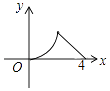 D、
D、
二、填空题
-
14. 2017年我国约有9400000人参加高考,将9400000用科学记数法表示为 .15. 分解因式:a2b﹣2ab+b= .16. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上,以原点O为位似中心,画△A1B1C1 , 使它与△ABC的相似比为2,则点B的对应点B1的坐标是 .
 17. 如图,点A为反比例函数y= 图象上一点,过A做AB⊥x轴于点B,连接OA则△ABO的面积为4,k= .
17. 如图,点A为反比例函数y= 图象上一点,过A做AB⊥x轴于点B,连接OA则△ABO的面积为4,k= . 18. 如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是 .
18. 如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是 .
三、解答题
-
19. 计算题(1)、计算:(﹣1)2017﹣4cos60°+ +(2)、先化简,再求值:(a﹣ )÷ ,其中a满足a2+3a﹣1=0.20. 为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
进球数(个)
人数
0
1
1
2
2
x
3
y
4
4
5
2
 (1)、求这个班级的男生人数;(2)、补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;(3)、该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有人.21. 十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措.二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(生男生女机会均等,且与顺序有关).(1)、该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好是1男1女的概率;(2)、该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中至少有1个女孩的概率.22. 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)、求这个班级的男生人数;(2)、补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;(3)、该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有人.21. 十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措.二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(生男生女机会均等,且与顺序有关).(1)、该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好是1男1女的概率;(2)、该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中至少有1个女孩的概率.22. 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上). (1)、求办公楼AB的高度;(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(1)、求办公楼AB的高度;(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:sin22°≈ ,cos22°≈ ,tan22≈ )
23. 在我市双城同创的工作中,某社区计划对1200m2的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为300m2区域的绿化时,甲队比乙队少用3天.(1)、甲、乙两施工队每天分别能完成绿化的面积是多少?(2)、设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数关系式.(3)、若甲队每天绿化费用为0.4万元,乙队每天绿化费用为0.15万元,且甲、乙两队施工的总天数不超过14天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.24. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G. (1)、求证:DF是⊙O的切线;(2)、若CF=1,DF= ,求图中阴影部分的面积.25. 抛物线y= x2+bx+c经过点A(﹣4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.
(1)、求证:DF是⊙O的切线;(2)、若CF=1,DF= ,求图中阴影部分的面积.25. 抛物线y= x2+bx+c经过点A(﹣4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧. (1)、求D点坐标;(2)、若∠PBA= ∠OBC,求点P的坐标;(3)、设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.
(1)、求D点坐标;(2)、若∠PBA= ∠OBC,求点P的坐标;(3)、设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.