2017年广西贵港市港南区中考数学一模试卷

试卷更新日期：2017-07-18 类型：中考模拟

进入出卷网下载

一、选择题

1. $\frac{1}{3}$ 的相反数是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下列运算正确的是（）

A、﹣3a+a=﹣2a B、a⁶÷a³=a² C、 $\sqrt{8}$ + $\sqrt{2}$ =10 D、（﹣2a²b³）²=4a⁴b⁵

查看试题解析
3. 已知1微米=10^﹣⁷米，则25微米用科学记数法表示为（）

A、0.25×10^﹣⁵米 B、25×10^﹣⁷米 C、2.5×10^﹣⁶米 D、2.5×10^﹣⁸米

查看试题解析
4. 下列命题中正确的是（）

A、正五边形是中心对称图形 B、平分弦的直径垂直于弦 C、化简﹣a $\sqrt{- \frac{1}{a}}$ 的结果是 $\sqrt{- a}$ D、顺次连接对角线互相垂直的四边形各边中点所得的四边形是菱形

查看试题解析
5. 2017年春学期小红同学四次中考数学测试成绩分别是：103，103，105，105，关于这组数据下列说法错误的是（）

A、平均数是104 B、众数是103 C、中位数是104 D、方差是1

查看试题解析
6. 用两种正多边形镶嵌，不能与正三角形匹配的正多边形是（）

A、正方形 B、正六边形 C、正八边形 D、正十二边形

查看试题解析
7. 若关于x的分式方程 $\frac{m - 1}{x - 1}$ =2的解为非负数，则m的取值范围是（）

A、m＞﹣1 B、m≥1 C、m＞﹣1且m≠1 D、m≥﹣1且m≠1

查看试题解析
8. 如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、3

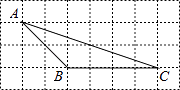查看试题解析
9. 已知反比例函数y= $\frac{1 - 2 m}{x}$ 的图象上有两点A（x₁ ， y₁），B（x₂ ， y₂），当x₁＜0＜x₂时，有y₁＜y₂ ，则m的取值范围是（）

A、m＜0 B、m＞0 C、m＜ $\frac{1}{2}$ D、m＞ $\frac{1}{2}$

查看试题解析
10. 如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（）

A、14 B、15 C、16 D、17

查看试题解析
11.
如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=40°，N是弧MB的中点，P是直径AB上的一动点，PM+PN的最小值为（）

A、4 $\sqrt{3}$ +1 B、4 $\sqrt{3}$ C、4 $\sqrt{2}$ +1 D、5

查看试题解析
12. 如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：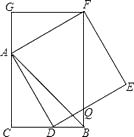

①AC=FG； ②S_△_FAB：S_{四边形CBFG}=1：2；
③∠ABC=∠ABF； ④AD²=FQ•AC，
其中正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 计算：2﹣3= ．

查看试题解析
14. 函数y= $\frac{1}{\sqrt{x - 3}}$ 自变量的取值范围是．

查看试题解析
15. 分解因式：4x²﹣16= ．

查看试题解析
16. 已知圆柱的侧面积是20π cm² ，高为5cm，则圆柱的底面半径为．

查看试题解析
17. 如图等边三角形ABC内接于圆，点P是圆上任意一点（P不与A、B、C重合），则∠APB= ．

查看试题解析
18.
如图，分别过点P_i（i，0）（i=1、2、…、n）作x轴的垂线，交 $y = \frac{1}{2} x^{2}$ 的图象于点A_i ，交直线 $y = - \frac{1}{2} x$ 于点B_i ．则 $\frac{1}{A_{1} B_{1}} + \frac{1}{A_{2} B_{2}} + \dots + \frac{1}{A_{n} B_{n}}$ = ．

查看试题解析

三、解答题

19. 结算题

(1)、计算：|1﹣ $\sqrt{3}$ |+3tan30°﹣（2017﹣π）⁰﹣（﹣ $\frac{1}{3}$ ）^﹣¹ ．

(2)、已知x、y满足方程组 ${\begin{matrix} 2 x - y = 1 \\ - x + 2 y = 2 \end{matrix}$ ，求代数式 $\frac{1}{x - 1}$ • $\frac{x^{2} - 1}{x + y}$ ﹣ $\frac{x}{x + y}$ 的值．

查看试题解析
20. 如图AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺按要求画图．

(1)、在图1中，画出△ABC的三条高的交点；

(2)、在图2中，画出△ABC中AB边上的高．

查看试题解析
21. 如图，在平面直角坐标系中，一次函数y=ax﹣a（a为常数）的图象与y轴相交于点A，与函数 $y = \frac{2}{x}$ 的图象相交于点B（m，1）．

(1)、求点B的坐标及一次函数的解析式；

(2)、若点P在y轴上，且△PAB为直角三角形，请直接写出点P的坐标．

查看试题解析
22.
今年4月23日，是第16个世界读书日．某校为了解学生每周课余自主阅读的时间，在本校随机抽取若干名学生进行问卷调查，现将调查结果绘制成如图不完整的统计图表，请根据图表中的信息解答下列问题
组别
学习时间x（h）
频数（人数）
A
0＜x≤1
8
B
1＜x≤2
24
C
2＜x≤3
32
D
3＜x≤4
n
E
4小时以上
4

(1)、表中的n= ，中位数落在组，扇形统计图中B组对应的圆心角为°；

(2)、请补全频数分布直方图；

(3)、该校准备召开利用课余时间进行自主阅读的交流会，计划在E组学生中随机选出两人进行经验介绍，已知E组的四名学生中，七、八年级各有1人，九年级有2人，请用画树状图法或列表法求抽取的两名学生都来自九年级的概率．

查看试题解析
23. 甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天，且甲队单独施工45天和乙队单独施工30天的工作量相同．

(1)、甲、乙两队单独完成此项任务需要多少天？

(2)、若甲、乙两队共同工作了3天后，乙队因设备检修停止施工，由甲队继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？

查看试题解析
24. 已知：如图，以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E，过点D作DF⊥BC，垂足为F．

(1)、求证：DF为⊙O的切线；

(2)、若等边三角形ABC的边长为4，求图中阴影部分的面积．

查看试题解析
25.
如图，抛物线y=﹣x²+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．

(1)、求经过A，B，C三点的抛物线的函数表达式；

(2)、点P是线段BD上一点，当PE=PC时，求点P的坐标；

(3)、在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、N、G为顶点的四边形是正方形时，请求出点M的坐标．

查看试题解析
26. △ABC中，AB=AC，D为BC的中点，以D为顶点作∠MDN=∠B．

(1)、
如图（1）当射线DN经过点A时，DM交AC边于点E，不添加辅助线，写出图中所有与△ADE相似的三角形．

(2)、
如图（2），将∠MDN绕点D沿逆时针方向旋转，DM，DN分别交线段AC，AB于E，F点（点E与点A不重合），不添加辅助线，写出图中所有的相似三角形，并证明你的结论．

(3)、
在图（2）中，若AB=AC=10，BC=12，当S_△_DEF= $\frac{1}{4}$ S_△_ABC时，求线段EF的长．

查看试题解析

组别	学习时间x（h）	频数（人数）
A	0＜x≤1	8
B	1＜x≤2	24
C	2＜x≤3	32
D	3＜x≤4	n
E	4小时以上	4