2017年广西贵港市港南区中考数学二模试卷
试卷更新日期:2017-07-18 类型:中考模拟
一、选择题
-
1. ﹣2017的倒数是( )A、2017 B、 C、﹣ D、02. 若点A(a﹣2,3)和点B(﹣1,b+5)关于y轴对称,则点C(a,b)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知 ,则 的值是( )A、 B、 C、 D、4. 若等腰三角形的两条边的长分别为5cm和8cm,则它的周长是( )A、13cm B、18cm C、21cm D、18cm或21cm5. 下列命题中,真命题的个数是( )
①同位角相等
②经过一点有且只有一条直线与这条直线平行
③长度相等的弧是等弧
④顺次连接菱形各边中点得到的四边形是矩形.
A、1个 B、2个 C、3个 D、4个6. 在同一直角坐标系中,若直线y=k1x与双曲线y= 没有公共点,则( )A、k1k2<0 B、k1k2>0 C、k1+k2<0 D、k1+k2>07. 若一元二次方程ax2﹣c=0(ac>0)的两个根分别是n+1与2n﹣4,则 =( )A、﹣2 B、1 C、2 D、48. 已知不等式组 仅有2个整数解,那么a的取值范围是( )A、a≥2 B、a<4 C、2≤a<4 D、2<a≤49. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( ) A、 B、 C、 D、10. 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A、 B、 C、 D、10. 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( ) A、12.5° B、15° C、20° D、22.5°11. 如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B﹣C﹣D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )
A、12.5° B、15° C、20° D、22.5°11. 如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B﹣C﹣D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )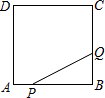 A、
A、 B、
B、 C、
C、 D、
D、 12. 如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE= ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF . 正确的个数是( )
12. 如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE= ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF . 正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知a2﹣b2=5,a+b=﹣2,那么代数式a﹣b的值 .14. 二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 .15. 如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B= .
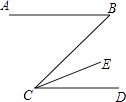 16. 如图,在Rt△ABC中,∠CAB=30°,∠C=90°.AD= AC,AB=8,E是AB上任意一点,F是AC上任意一点,则折线DEFB的最短长度为 .
16. 如图,在Rt△ABC中,∠CAB=30°,∠C=90°.AD= AC,AB=8,E是AB上任意一点,F是AC上任意一点,则折线DEFB的最短长度为 . 17. 如图,在平面直角坐标系中,直线l:y= x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴的正半轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A6B7A7的周长是 .
17. 如图,在平面直角坐标系中,直线l:y= x+1交x轴于点A,交y轴于点B,点A1、A2、A3 , …在x轴的正半轴上,点B1、B2、B3 , …在直线l上.若△OB1A1 , △A1B2A2 , △A2B3A3 , …均为等边三角形,则△A6B7A7的周长是 .
三、解答题
-
18. 计算题(1)、(π﹣2017)0+|2﹣ |﹣4cos30°+(2)、先化简,再求值: ﹣ ÷ ,其中a= .19. 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4)、B(3,﹣2)、C(6,﹣3).(1)、①画出△ABC关于x轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2:1.
(2)、直接写出C2的坐标.20. 如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数 (k≠0)的图象上. (1)、求a的值;(2)、直接写出点P′的坐标;(3)、求反比例函数的解析式.21. 2016年3月,我校举办了以“读城记”为主题的校读书节暨文化艺术节,为了解初中学生更喜欢下列A、B、C、D哪个比赛,从初中学生随机抽取了部分学生进行调查,每个参与调查的学生只选择最喜欢的一个项目,并把调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)、求a的值;(2)、直接写出点P′的坐标;(3)、求反比例函数的解析式.21. 2016年3月,我校举办了以“读城记”为主题的校读书节暨文化艺术节,为了解初中学生更喜欢下列A、B、C、D哪个比赛,从初中学生随机抽取了部分学生进行调查,每个参与调查的学生只选择最喜欢的一个项目,并把调查结果绘制了两幅不完整的统计图,请回答下列问题:
A.“寻找星主播”校园主持人大赛
B.“育才音超”校园歌手大赛
C.阅读之星评选
D.“超级演说家”演讲比赛
(1)、这次被调查的学生共有人.请你将统计图补充完整 .(2)、在此调查汇总,抽到了七年级(1)班3人.其中2人喜欢“育才音超”校园歌手大赛、1人喜欢阅读之星评选.抽到八年级(5)班2人,其中1人喜欢“超级演说家”演讲比赛、1人喜欢阅读之星评选.从这5人中随机选两人.用列表或用树状图求出两人都喜欢阅读之星评选的概率.22. 小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.(1)、每个篮球和足球各需多少元?(2)、根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?23. 已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF. (1)、求证:EF是⊙O的切线;(2)、若⊙O的半径为3,∠EAC=60°,求AD的长.24. 如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B(3,0).
(1)、求证:EF是⊙O的切线;(2)、若⊙O的半径为3,∠EAC=60°,求AD的长.24. 如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B(3,0). (1)、求b、c的值;(2)、如图1直线y=kx+1(k>0)与抛物线第一象限的部分交于D点,交y轴于F点,交线段BC于E点.求 的最大值;(3)、如图2,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.问在直线BC下方的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.25. △ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)、观察猜想
(1)、求b、c的值;(2)、如图1直线y=kx+1(k>0)与抛物线第一象限的部分交于D点,交y轴于F点,交线段BC于E点.求 的最大值;(3)、如图2,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.问在直线BC下方的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.25. △ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)、观察猜想如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
 (2)、数学思考
(2)、数学思考如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
 (3)、拓展延伸
(3)、拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ,CD= BC,请求出GE的长.
