2017年河北省承德市六校中考数学一模试卷
试卷更新日期:2017-07-18 类型:中考模拟
一、选择题
-
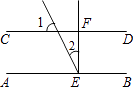
1. ﹣3的绝对值是( )A、3 B、﹣3 C、 D、2. 一个等腰三角形的两边长分别是3和7,则它的周长为( )A、17 B、15 C、13 D、13或173. 据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )A、0.3×106 B、3×105 C、3×106 D、30×1044. 如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=60°,则∠2=( )
 A、20° B、60° C、30° D、45°5. 估算 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 如图是几何体的三视图,该几何体是( )
A、20° B、60° C、30° D、45°5. 估算 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 如图是几何体的三视图,该几何体是( )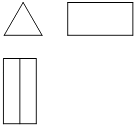 A、圆锥 B、圆柱 C、正三棱柱 D、正三棱锥7. 下列计算中,正确的是( )A、x2+x4=x6 B、2x+3y=5xy C、(x3)2=x6 D、x6÷x3=x28. 如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )
A、圆锥 B、圆柱 C、正三棱柱 D、正三棱锥7. 下列计算中,正确的是( )A、x2+x4=x6 B、2x+3y=5xy C、(x3)2=x6 D、x6÷x3=x28. 如图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )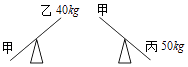 A、
A、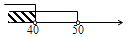 B、
B、 C、
C、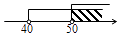 D、
D、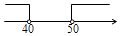 9. 如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
9. 如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )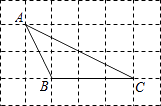 A、 B、 C、 D、10. 方程 的解为( )A、x= B、x= C、x=﹣2 D、无解11. 如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )
A、 B、 C、 D、10. 方程 的解为( )A、x= B、x= C、x=﹣2 D、无解11. 如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )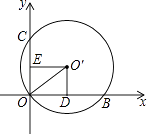 A、7 B、6 C、5 D、412. 某篮球队12名队员的年龄如表所示:
A、7 B、6 C、5 D、412. 某篮球队12名队员的年龄如表所示:年龄(岁)
18
19
20
21
人数
5
4
1
2
则这12名队员年龄的众数和中位数分别是( )
A、18,19 B、18,19.5 C、5,4 D、5,4.513. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠B=25°,则∠ACB的度数为( )
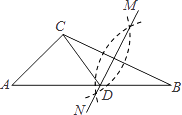 A、90° B、95° C、100° D、105°14. 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
A、90° B、95° C、100° D、105°14. 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )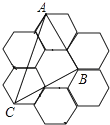 A、 B、2 C、3 D、315. 如图,在△ABC中,AB=AC=a,∠BAC=18°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=99°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )
A、 B、2 C、3 D、315. 如图,在△ABC中,AB=AC=a,∠BAC=18°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=99°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( ) A、
A、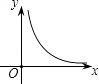 B、
B、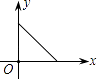 C、
C、 D、
D、 16. 对于问题:证明不等式a2+b2≥2ab,甲、乙两名同学的作业如下:
16. 对于问题:证明不等式a2+b2≥2ab,甲、乙两名同学的作业如下:甲:根据一个数的平方是非负数可知(a﹣b)2≥0,
∴a2﹣2ab+b2≥0,
∴a2+b2≥2ab.
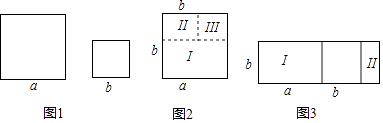
乙:如图1,两个正方形的边长分别为a、b(b≤a),如图2,先将边长为a的正方形沿虚线部分分别剪成Ⅰ、Ⅱ、Ⅲ三部分,若再将Ⅰ、Ⅱ和边长为b的正方形拼接成如图3所示的图形,可知此时图3的面积为2ab,其面积小于或等于原来两个正方形的面积和,故不等式a2+b2≥2ab成立.
则对于两人的作业,下列说法正确的是( )
 A、甲、乙都对 B、甲对,乙不对 C、甲不对,乙对 D、甲、乙都不对
A、甲、乙都对 B、甲对,乙不对 C、甲不对,乙对 D、甲、乙都不对二、填空题
-
17. 计算23的结果是 .18. 已知a﹣b=3,则a(a﹣2b)+b2的值为 .19. 在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).(1)、点( , )的“双角坐标”为;(2)、若点P到x轴的距离为 ,则m+n的最小值为 .
三、解答题
-
20. 以下是一位同学所做的实数运算解题过程的一部分.
﹣ ﹣|﹣1|2017﹣(π﹣3.14)0+4cos60°
=﹣ +1﹣1+4× .
(1)、指出上面解答过程中的错误,并写出正确的解答过程;(2)、若分式方程 +1= 的解与(1)中的最终结果相同,求a的值.21. 如图,在Rt△ABC中,∠C=90°,BC=8,tanB= ,点D在BC上,且BD=AD,求AC的长和cos∠ADC的值.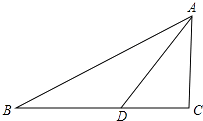 22. 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
22. 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.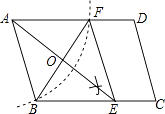 (1)、求证:四边形ABEF为菱形;(2)、AE,BF相交于点O,若BF=6,AB=5,求AE的长.23. 2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)、求证:四边形ABEF为菱形;(2)、AE,BF相交于点O,若BF=6,AB=5,求AE的长.23. 2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题: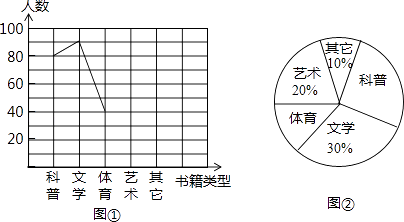 (1)、在这次抽样调查中,一共调查了多少名学生?(2)、请把折线统计图(图1)补充完整;(3)、求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(1)、在这次抽样调查中,一共调查了多少名学生?(2)、请把折线统计图(图1)补充完整;(3)、求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)、如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.24. 如图,点A(m,m+1),B(m+3,m﹣1)都在反比例函数 的图象上.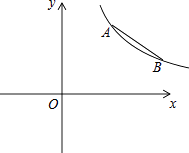 (1)、求m,k的值;(2)、求直线AB的函数表达式;(3)、如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,直接写出点M,N的坐标.25. 在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= AD,点N是折线AB﹣BC上的一个动点.
(1)、求m,k的值;(2)、求直线AB的函数表达式;(3)、如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,直接写出点M,N的坐标.25. 在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM= AD,点N是折线AB﹣BC上的一个动点.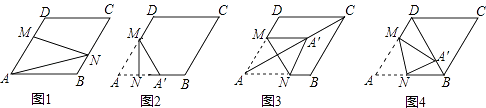 (1)、如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .(2)、当点N在AB边上时,将△AMN沿MN翻折得到
(1)、如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .(2)、当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求 的值.
26. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资成本x成正比例关系,种植花卉的利润y2与投资成本x的平方成正比例关系,并得到了表格中的数据;投资量x(万元)
2
种植树木的利润y1(万元)
4
种植花卉的利润y2(万元)
2
(1)、分别求出利润y1与y2关于投资量x的函数关系式;(2)、如果这位专业户计划以8万元资金投入种植花卉和树木,设他投入种植花卉金额万元,种植花卉和树木共获利润W万元,求出W与m之间的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?(3)、若该专业户想获利不低于22万元,在(2)的条件下,求出投资种植花卉的金额m的范围.