2017年广西桂林市中考数学二模试卷
试卷更新日期：2017-07-18 类型：中考模拟
一、选择题
-
1. 下列四个数中，最小的数是（ ）A、﹣1 B、0 C、1 D、22. 点P（2，﹣3）在第（ ）象限．
A、四 B、三 C、二 D、一3. 如图，直线a∥b，点B在直线a上，AB⊥BC，若∠1=38°，则∠2的度数为（ ）
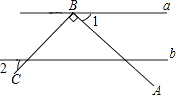A、38° B、52° C、76° D、142°4. 用5个完全相同的小正方体组合成如图所示的立体图形，它的俯视图是（ ）
A、
B、
C、
D、
5. 若﹣x3ya与xby是同类项，则a+b的值为（ ）A、5 B、4 C、3 D、26. 每到四月，许多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰，据测定，杨絮纤维的直径约为0.0000105m，该数值用科学记数法表示为（ ）A、1.05×105 B、1.05×10﹣5 C、0.105×10﹣5 D、10.5×10﹣47. 面积为5的正方形的边长在（ ）A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间8. 下列说法正确的是（ ）A、了解飞行员视力的达标标率应使用抽样调查 B、从2000名学生中选出200名学生进行抽样调查，样本容量为2000 C、一组数据3，6，6，7，9的中位数是6 D、一组数据1，2，3，4，5的方差是109. 下列命题中，真命题的个数是（ ）①同位角相等；②经过直线外一点有且只有一条直线与这条直线平行；③长度相等的弧是等弧；④顺次连接菱形各边中点得到的四边形是矩形．
A、1个 B、2个 C、3个 D、4个10. 如图，圆锥底面半径为rcm，母线长为5cm，其侧面展开图是圆心角为216°的扇形，则r的值为（ ）
A、3 B、4 C、5 D、611. 如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①b2﹣4ac＜0；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③2a+b=0；④当y＞0时，x的取值范围是﹣1＜x＜3；⑤当x＞0时，y随x增大而减小．其中结论正确的个数是（ ）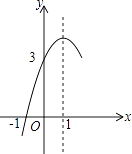
A、4个 B、3个 C、2个 D、1个12. 如图，将边长为2的等边△OAB放置于平面直角坐标系xOy中，C是AB边上的一个点（不与端点A、B重合），作CD⊥OB于点D，若点C、D都在双曲线y= 上（k＞0，x＞0），则k的值为（ ）
A、 B、 C、 D、二、填空题
-
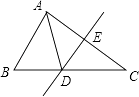
13. 分解因式：a2﹣3a= ．14. 已知点M（1，a）和点N（2，b）是一次函数y=﹣2x+1图象上的两点，则a与b的大小关系是：ab（填“＜”，“=”，或“＞”）15. 如图，在△ABC中，DE是AC的垂直平分线，点D在BC上，△ABC的周长为20cm，△ABD的周长为12cm，则AE的长为 cm．
16. 如图，在扇形AOB中，∠AOB=90°，正方形CDEF的顶点C是弧AB的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2时，阴影部分的面积为 ．
17. 如图，在四边形ABCD中，对角线AC、BD相交于点E，∠DAB=∠CDB=90°，∠ABD=45°，∠DCA=30°，AB=6，则AE= ．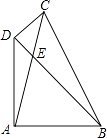
18. 如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=1，OC= ，在第二象限内，以原点O为位似中心将矩形AOCB放大为原来的 倍，得到矩形A1OC1B1 ， 再以原点O为位似中心将矩形A1OC1B1放大为原来的 倍，得到矩形A2OC2B2…，以此类推，得到的矩形A100OC100B100的对角线交点的纵坐标为 ．
三、解答题
-
19. 计算：（π﹣5）0+cos45°﹣|﹣ |+ ．20. 解方程组： ．21. 如图，已知△ABC中，AB=AC，BD、CE是高，BD与CE相交于点O．
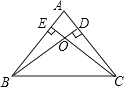(1)、求证：BD=CE；(2)、若∠A=80°，求∠BOC的度数．22. 某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况，随机调查了若干名学生，根据调查数据进行整理，绘制了如下的不完整统计图．
请你根据以上的信息，回答下列问题：
(1)、本次共调查了名学生，其中最喜爱体育的有人；(2)、在扇形统计图中，最喜爱体育的对应扇形的圆心角大小是 ．(3)、小李和小张在新闻、体育、动画三类电视节目中分别有一类是自己最喜爱的节目，请用树状图或列表法求两人恰好最喜爱同一类节目的概率．23. 如图，矩形ABCD的长AD=5cm，宽AB=3cm，长和宽都增加xcm，那么面积增加ycm2 ．
(1)、写出y与x的函数关系式；(2)、当增加的面积y=20cm2时，求相应的x是多少？24.如图，在大楼AB的正前方有一斜坡CD，已知斜坡CD长6 米，坡角∠DCE等于45°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的顶点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．
(1)、求斜坡CD的高度DE；(2)、求大楼AB的高度（结果保留根号）．25. 已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，过点B作BK⊥AC，垂足为K，过D作DH∥KB，DH分别与AC，AB，⊙O及CB的延长线相交于点E，F，G，H，且F是EG的中点．
(1)、求证：点D在⊙O上；(2)、求证：F是AB的中点；(3)、若DE=4，求⊙O的半径和△BFH的面积．26. 如图，抛物线y=ax2+bx﹣2经过点A（1，0）和点B（4，0），与y轴交于点C．附：阅读材料
法国弗朗索瓦•韦达最早发现一元二次方程中根与系数的关系为：两根之和等于一次项系数与二次项系数之比的相反数，两根之积等于常数项羽二次项系数之比，人们称之为韦达定理．
即：设一元二次方程ax2+bx+c=0的两根为x1、x2 ， 则：x1+x2=﹣ ，x1•x2= 能灵活运用韦达定理，有时可以使解题更为简单．
(1)、求抛物线的解析式；(2)、以点A为圆心，作于直线BC相切的⊙A，求⊙A的面积；(3)、将直线BC向下平移n个单位后与抛物线交于点M、N，且线段MN=2CB，求直线MN的解析式及平移距离．