2017年广东省深圳市南山区中考数学二模试卷
试卷更新日期:2017-07-18 类型:中考模拟
一、选择题
-
1. 下列四个数中,最大的数是( )A、﹣2 B、 C、0 D、62. 下列运算正确的是( )A、a2•a3=a6 B、(a2)3=a5 C、(﹣2a2b)3=﹣8a6b3 D、(2a+1)2=4a2+2a+13. “互联网”已全面进入人们的日常生活,据有关部门统计,目前全国4G用户数达到4.62亿,其中4.62亿用科学记数法表示为( )A、4.62×104 B、4.62×106 C、4.62×108 D、0.462×1084. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
5. 陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( ) A、19 B、18 C、16 D、156. 下列说法正确的是( )
A、19 B、18 C、16 D、156. 下列说法正确的是( )①面积之比为1:2的两个相似三角形的周长之比是1:4;②三视图相同的几何体是正方体;③﹣27没有立方根;④对角线互相垂直的四边形是菱形;⑤某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为 =82分, =82分,S2甲=245,S2乙=190,那么成绩较为整齐的是乙班.
A、1个 B、2个 C、3个 D、4个7. 如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1 , 则a+b的值为( ) A、2 B、3 C、4 D、58. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
A、2 B、3 C、4 D、58. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0;
④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
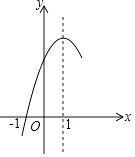 A、4个 B、3个 C、2个 D、1个9. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
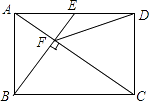
A、4个 B、3个 C、2个 D、1个9. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= .
其中正确的结论有( )
 A、4个 B、3个 C、2个 D、1个10. 如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
A、4个 B、3个 C、2个 D、1个10. 如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )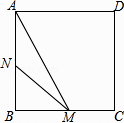 A、
A、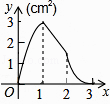 B、
B、 C、
C、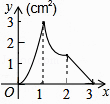 D、
D、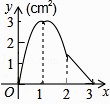
二、填空题
-
11. 已知a+b=3,a﹣b=5,则代数式a2﹣b2的值是 .12. 如图,已知正方形ABCD的边长为2.如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′点处,那么tan∠BAD′等于 .
 13. 如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是 .
13. 如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是 . 14. 如图,已知点A是双曲线 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线 上运动,则k的值是 .
14. 如图,已知点A是双曲线 在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线 上运动,则k的值是 .
三、解答题
-
15. 化简: ,然后在不等式x≤2的非负整数解中选择一个适当的数代入求值.16. 计算:(﹣1)2016+2sin60°﹣|﹣ |+π0 .17. 黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
 (1)、本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;(2)、本次抽样调查中,学习时间的中位数落在哪个等级内?(3)、表示B等级的扇形圆心角α的度数是多少?(4)、在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.18. 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)、本次抽样调查共抽取了多少名学生?并将条形统计图补充完整;(2)、本次抽样调查中,学习时间的中位数落在哪个等级内?(3)、表示B等级的扇形圆心角α的度数是多少?(4)、在此次问卷调查中,甲班有2人平均每天课外学习时间超过2小时,乙班有3人平均每天课外学习时间超过2小时,若从这5人中任选2人去参加座谈,试用列表或化树状图的方法求选出的2人来自不同班级的概率.18. 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系. (1)、求y与x的函数关系式;(2)、若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.19. 如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离( 取1.73,结果精确到0.1千米)
(1)、求y与x的函数关系式;(2)、若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.19. 如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离( 取1.73,结果精确到0.1千米)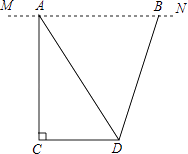 20. 如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
20. 如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB. (1)、求证:CE⊥AB;(2)、求证:PC是⊙O的切线;(3)、若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.21. 如图,抛物线y=﹣x2+(m﹣1)x+m(m>1)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,3).
(1)、求证:CE⊥AB;(2)、求证:PC是⊙O的切线;(3)、若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.21. 如图,抛物线y=﹣x2+(m﹣1)x+m(m>1)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C(0,3). (1)、求抛物线的解析式;(2)、点D和点C关于抛物线的对称轴对称,点你F在直线AD上方的抛物线上,FG⊥AD于G,FH∥x轴交直线AD于H,求△FGH的周长的最大值;(3)、点M是抛物线的顶点,直线l垂直于直线AM,与坐标轴交于P、Q两点,点R在抛物线的对称轴上,使得△PQR是以PQ为斜边的等腰直角三角形,求直线l的解析式.
(1)、求抛物线的解析式;(2)、点D和点C关于抛物线的对称轴对称,点你F在直线AD上方的抛物线上,FG⊥AD于G,FH∥x轴交直线AD于H,求△FGH的周长的最大值;(3)、点M是抛物线的顶点,直线l垂直于直线AM,与坐标轴交于P、Q两点,点R在抛物线的对称轴上,使得△PQR是以PQ为斜边的等腰直角三角形,求直线l的解析式.