2017年广东省中考数学模拟试卷(二)
试卷更新日期:2017-07-18 类型:中考模拟
一、选择题
-
1. |﹣2|=( )A、2 B、﹣2 C、 D、2. 据报道,2015年第一季度,广东省实现地区生产总值约1560 000 000 000元,用科学记数法表示为( )A、0.156×1012元 B、1.56×1012元 C、1.56×1011元 D、15.6×1011元3. 一组数据:2,5,4,3,2的中位数是( )A、4 B、3.2 C、3 D、24. 如图,直线l1∥l2 , CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
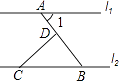 A、50° B、45° C、40° D、30°5. 下列所给图形是中心对称图形但不是轴对称图形的是( )A、
A、50° B、45° C、40° D、30°5. 下列所给图形是中心对称图形但不是轴对称图形的是( )A、 B、
B、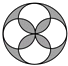 C、
C、 D、
D、 6. 下列运算正确的是( )A、 =±2 B、 =﹣16 C、x6÷x3=x2 D、(2x2)3=8x67. 一次函数y=﹣2x+3的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为﹣1、3,则下列说法错误的是( )
6. 下列运算正确的是( )A、 =±2 B、 =﹣16 C、x6÷x3=x2 D、(2x2)3=8x67. 一次函数y=﹣2x+3的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为﹣1、3,则下列说法错误的是( ) A、对称轴是直线x=1 B、方程ax2+bx+c=0的解是x1=﹣1,x2=3 C、当x<1,y随x的增大而增大 D、当﹣1<x<3时,y<09. 若关于x的一元二次方程x2﹣4x+(5﹣m)=0有实数根,则m的取值范围是( )A、m>1 B、m≥1 C、m<1 D、m≤110.
A、对称轴是直线x=1 B、方程ax2+bx+c=0的解是x1=﹣1,x2=3 C、当x<1,y随x的增大而增大 D、当﹣1<x<3时,y<09. 若关于x的一元二次方程x2﹣4x+(5﹣m)=0有实数根,则m的取值范围是( )A、m>1 B、m≥1 C、m<1 D、m≤110.如图,已知矩形ABCD中,R是边CD的中点,P是边BC上一动点,E、F分别是AP、RP的中点,设BP的长为x,EF的长为y,当P在BC上从B向C移动时,y与x的大致图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 分解因式:x2﹣9= .12. 不等式组 的解集是 .13. 分式方程 的解是 .14. 如图,菱形ABCD中,∠BCD=120°,AC=5,则菱形ABCD的周长是 .
 15. 如图,正方形ABCD的边长为9,将正方形折叠,使D点落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是 .
15. 如图,正方形ABCD的边长为9,将正方形折叠,使D点落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是 .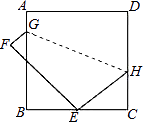 16. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为 .
16. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为 .
三、解答题
-
17. 解方程组: .18. 先化简,再求值: ﹣ ÷ ,其中x= ﹣1.19. 如图,已知△ABC,AC>BC.
 (1)、尺规作图:在AC边上求作一点P,使PB=PC(保留作图痕迹,不写作法);(2)、若BC=6,∠C=30°,求△PBC的面积.
(1)、尺规作图:在AC边上求作一点P,使PB=PC(保留作图痕迹,不写作法);(2)、若BC=6,∠C=30°,求△PBC的面积.四、解答题
-
20. 一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3,从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.(1)、请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;(2)、求两次摸出的球上的数字和为偶数的概率.21. 某玩具店购进一种儿童玩具,计划每个售价36元,能盈利80%,在销售中出现了滞销,于是先后两次降价,售价降为25元.(1)、求这种玩具的进价;(2)、求平均每次降价的百分率(精确到0.1%).22. 如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F.
 (1)、求证:△ADG≌△FDG;(2)、若BG=2AG,BD=2 ,求AD的长.
(1)、求证:△ADG≌△FDG;(2)、若BG=2AG,BD=2 ,求AD的长.五、解答题
-
23. 如图,在平面直角坐标系xOy中,直线y=kx+2与x轴、y轴分别交于点A(﹣1,0)和点B,与反比例函数y= 的图象在第一象限内交于点C(1,n).
 (1)、求k的值;(2)、求反比例函数的解析式;(3)、过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y= 交于点P、Q,且PQ=2QD,求点D的坐标.24. 如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.
(1)、求k的值;(2)、求反比例函数的解析式;(3)、过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y= 交于点P、Q,且PQ=2QD,求点D的坐标.24. 如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M. (1)、求证:四边形ABCD是矩形;(2)、若点G为MF的中点,求证:BG是⊙O的切线;(3)、若AD=4,CM=9,求四边形ABCD的面积.25.
(1)、求证:四边形ABCD是矩形;(2)、若点G为MF的中点,求证:BG是⊙O的切线;(3)、若AD=4,CM=9,求四边形ABCD的面积.25.如图1,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图1所示的位置绕G点沿逆时针方向旋转α(0°<α<90°),如图2,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题:
 (1)、求证:△CGH∽△AGK;
(1)、求证:△CGH∽△AGK;
(2)、连接HK,求证:KH∥EF;
 (3)、设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值.
(3)、设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值.