2017年广东省惠州市惠阳区中考数学模拟试卷
试卷更新日期:2017-07-18 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、﹣2 B、2 C、 D、2. 下列图案中既是中心对称图形,又是轴对称图形的是( )A、
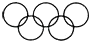 B、
B、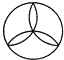 C、
C、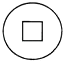 D、
D、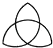 3. 2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )A、32,31 B、31,32 C、31,31 D、32,354. 如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )
3. 2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )A、32,31 B、31,32 C、31,31 D、32,354. 如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为( )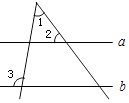 A、35° B、45° C、50° D、55°5. 下列运算正确的是( )A、2a+3b=5ab B、a2•a3=a5 C、(2a)3=6a 3 D、a6+a3=a96. 一元二次方程x2﹣4x+2=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 若等腰三角形的两边长为3和7,则该等腰三角形的周长为( )A、10 B、13 C、17 D、13或178. 不等式组 的解集在数轴上表示正确的是( )A、
A、35° B、45° C、50° D、55°5. 下列运算正确的是( )A、2a+3b=5ab B、a2•a3=a5 C、(2a)3=6a 3 D、a6+a3=a96. 一元二次方程x2﹣4x+2=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 若等腰三角形的两边长为3和7,则该等腰三角形的周长为( )A、10 B、13 C、17 D、13或178. 不等式组 的解集在数轴上表示正确的是( )A、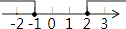 B、
B、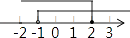 C、
C、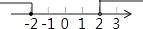 D、
D、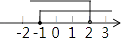
二、填空题
-
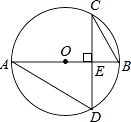
9. 因式分解:x2﹣36= .10. 一个多边形的内角和为1080°,则这个多边形的边数是 .11. 若△ABC∽△A′B′C′,相似比为1:3,则△ABC与△A′B′C′的面积之比为 .12. 分式方程 的解是 .13. 如图,在⊙O中,CD⊥AB于E,若∠BAD=30°,且BE=2,则CD= .
 14. 如图,在圆心角为90°的扇形OAB中,半径OA=4,C为 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 .
14. 如图,在圆心角为90°的扇形OAB中,半径OA=4,C为 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 .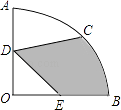
三、解答题
-
15. 计算:(﹣ )﹣1﹣| ﹣1|+3tan30°+(2017﹣π)0 .16. 先化简,再求值:
( ) ,请在﹣3,0,1,3中选择一个适当的数作为x值.
17. 如图,△ABC中,∠C=90°,∠A=30°.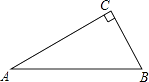 (1)、用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)(2)、连接BD,求证:DE=CD.
(1)、用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)(2)、连接BD,求证:DE=CD.四、解答题
-
18. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
 (1)、这次被调查的学生共有人;(2)、请你将条形统计图补充完成;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).19. 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ≈1.73,精确到个位)
(1)、这次被调查的学生共有人;(2)、请你将条形统计图补充完成;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).19. 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ≈1.73,精确到个位)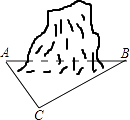 20. 某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.(1)、求该种商品每次降价的百分率;(2)、若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
20. 某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.(1)、求该种商品每次降价的百分率;(2)、若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?五、解答题
-
21. 直线y=kx+b与反比例函数y= (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
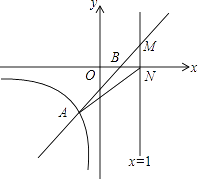 (1)、求m的值;(2)、求直线AB的解析式;(3)、若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ,求t的值.22. 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)、求m的值;(2)、求直线AB的解析式;(3)、若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ,求t的值.22. 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.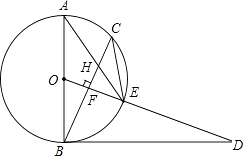 (1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= ,求BH的长.23. 把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).
(1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= ,求BH的长.23. 把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s). (1)、用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;(2)、连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;(3)、当t为何值时,△APQ是等腰三角形.
(1)、用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;(2)、连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;(3)、当t为何值时,△APQ是等腰三角形.