2017年甘肃省白银市靖远县中考数学二模试卷
试卷更新日期：2017-07-18 类型：中考模拟
一、选择题
-
1. ﹣ 的相反数是（ ）A、2 B、﹣2 C、 D、﹣2. 宇宙现在的年龄约为200亿年，200亿用科学记数法表示为（ ）A、0.2×1011 B、2×1010 C、200×108 D、2×1093. 下列计算正确的是（ ）A、x4+x4=x16 B、（﹣2a）2=﹣4a2 C、x7÷x5=x2 D、m2•m3=m64. 如图，直线a、b被直线c、d所截，若∠1=∠2，∠3=125°，则∠4的度数为（ ）
A、55° B、60° C、70° D、75°5. 一个几何体的三视图如图所示，那么这个几何体是（ ）
A、圆锥 B、圆柱 C、长方体 D、三棱柱6. 沅江市近年来大力发展芦笋产业，某芦笋生产企业在两年内的销售额从20万元增加到80万元．设这两年的销售额的年平均增长率为x，根据题意可列方程为（ ）A、20（1+2x）=80 B、2×20（1+x）=80 C、20（1+x2）=80 D、20（1+x）2=807. 一元二次方程2x2+3x+1=0的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定8. 如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴是直线x=﹣2．关于下列结论：①ab＜0；②b2﹣4ac＞0；③9a﹣3b+c＜0；④b﹣4a=0；⑤方程ax2+bx=0的两个根为x1=0，x2=﹣4，其中正确的结论有（ ）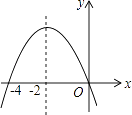
A、①③④ B、②④⑤ C、①②⑤ D、②③⑤9. 一个多边形的每个外角都等于60°，则这个多边形的边数为（ ）A、8 B、7 C、6 D、5二、填空题
-
10. 分解因式a2﹣9的结果是 ．11. 如图，△ABC中，DE是BC的垂直平分线，DE交AC于点E，连接BE．若BE=9，BC=12，则cosC= ．
12. 如果单项式﹣xyb+1与 xa﹣2y3是同类项，那么（a﹣b）2015= ．13. 化简：（1﹣x）2+2x= ．14. 一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根，则该等腰三角形的周长是 ．15. 如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD等于 ．
16. 如下图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段DE的长为 ．
17. 如图是由火柴棒搭成的几何图案，则第n个图案中有根火柴棒．（用含n的代数式表示）
三、解答题
-
18. 计算： +（π﹣3.14）0﹣tan60°+|1﹣ |．19.
如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为
A（﹣1，1），B（﹣3，1），C（﹣1，4）．
①画出△ABC关于y轴对称的△A1B1C1；
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 ， 请在图中画出△A2BC2 ， 并求出线段BC旋转过程中所扫过的面积（结果保留π）．
20. 如图，某农场有一块长40m，宽32m的矩形种植地，为方便管理，准备沿平行于两边的方向纵、横各修建一条等宽的小路，要使种植面积为1140m2 ， 求小路的宽．
21.如图，在一笔直的海岸线l上有A、B两个码头，A在B的正东方向，一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处，此时从B码头测得小船在它的北偏东45°的方向．求此时小船到B码头的距离（即BP的长）和A、B两个码头间的距离（结果都保留根号）．
22. 在一只不透明的袋中，装着标有数字3，4，5，7的质地、大小均相同的小球，小明和小东同时从袋中随机各摸出1个球，并计算这两个球上的数字之和，当和小于9时小明获胜，反之小东获胜．(1)、请用树状图或列表的方法，求小明获胜的概率；(2)、这个游戏公平吗？请说明理由．四、解答题
-
23. 为了了解市民“获取新闻的最主要途径”某市记者开展了一次抽样调查，根据调查结果绘制了如下尚不完整的统计图．
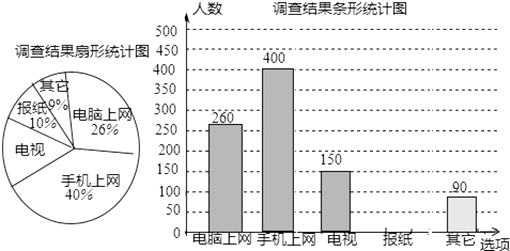
根据以上信息解答下列问题：
(1)、这次接受调查的市民总人数是；(2)、扇形统计图中，“电视”所对应的圆心角的度数是；(3)、请补全条形统计图；(4)、若该市约有80万人，请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数．24. 如图，一次函数y=kx+b的图象与反比例函数y= 的图象相交于点A（1，5）和点B，与y轴相交于点C（0，6）．
(1)、求一次函数和反比例函数的解析式；(2)、现有一直线l与直线y=kx+b平行，且与反比例函数y= 的图象在第一象限有且只有一个交点，求直线l的函数解析式．25. 如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．
(1)、求证：AE=DF；(2)、若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
