2017年安徽省宿州市埇桥区中考数学最后一卷
试卷更新日期:2017-07-18 类型:中考模拟
一、选择题
-
1. ﹣2017 的相反数是( )A、2017 B、 C、±2017 D、|﹣2017|2. 下列各式运算结果为a5的是( )A、(a2)3 B、a2+a3 C、a2•a3 D、a10÷a23. 3月5日,第十二届全国人民代表大会第五次会议上国务院总理李克强在政府工作报告中指出:回顾2016年,人民生活继续改善,城乡居民生活水平有新的提高,农村贫困人口减少1240万,其中数据1240万用科学记数法表示为( )A、1.24×103 B、12.4×102 C、1.24×107 D、12.4×1064. 如图所示的是由5个大小相同的圆柱搭成的几何体,其左视图是( )
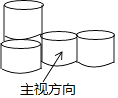 A、
A、 B、
B、 C、
C、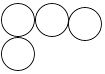 D、
D、 5. 如图,∠1+∠B=180°,∠2=45°,则∠D的度数是( )
5. 如图,∠1+∠B=180°,∠2=45°,则∠D的度数是( ) A、25° B、45° C、50° D、65°6. 某经济开发区今年一月份工业产值达到80亿元,第一季度总产值为275亿元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,根据题意所列方程是( )A、80(1+x)2=275 B、80+80(1+x)+80(1+x)2=275 C、80(1+x)3=275 D、80(1+x)+80(1+x)2=2757. 某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )
A、25° B、45° C、50° D、65°6. 某经济开发区今年一月份工业产值达到80亿元,第一季度总产值为275亿元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,根据题意所列方程是( )A、80(1+x)2=275 B、80+80(1+x)+80(1+x)2=275 C、80(1+x)3=275 D、80(1+x)+80(1+x)2=2757. 某单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制成如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵以上的人数占总人数的( )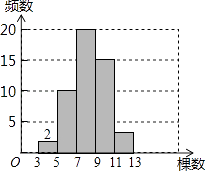 A、40% B、70% C、76% D、96%8. 如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A、40% B、70% C、76% D、96%8. 如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )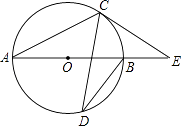 A、40° B、50° C、60° D、70°9. 随着互联网的发展,互联网消费逐渐深入人们的生活,如图所示的是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,有下列说法:其中正确说法的个数有( )
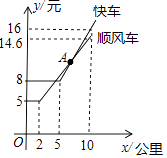
A、40° B、50° C、60° D、70°9. 随着互联网的发展,互联网消费逐渐深入人们的生活,如图所示的是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,有下列说法:其中正确说法的个数有( )①“快车”行驶里程不超过5公里计费8元;
②“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
③A点的坐标为(6.5,10.4);
④从合肥西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元.
 A、1个 B、2个 C、3个 D、4个10. 在△ABC纸片中,∠ACB=90°,AC=6,BC=8,沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,那么这个等腰三角形的面积不可能是( )A、14.4 B、19.2 C、18.75 D、17
A、1个 B、2个 C、3个 D、4个10. 在△ABC纸片中,∠ACB=90°,AC=6,BC=8,沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,那么这个等腰三角形的面积不可能是( )A、14.4 B、19.2 C、18.75 D、17二、填空题
-
11. 计算:﹣1+3= .12. 方程 = 的解是 .13. 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为
cm2 . (结果保留π)
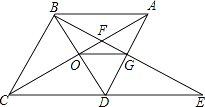
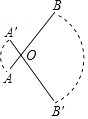 14. 如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上)
14. 如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上)①OG= AB;
②与△EGD全等的三角形共有5个;
③S四边形CDGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
三、解答题
-
15. 解不等式组 .16. 化简分式 ÷ ﹣1,并选取一个你认为合适的整数a代入求值.17.
如图,已知A(2,3)、B(1,1)、C(4,1)是平面直角坐标系中的三点.
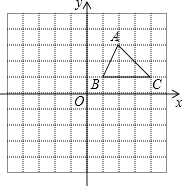 (1)、①请画出△ABC关于y轴对称的△A1B1C1;
(1)、①请画出△ABC关于y轴对称的△A1B1C1;②画出△A1B1C1向下平移3个单位得到的△A2B2C2;
(2)、若△ABC中有一点P坐标为(x,y),请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标.
18.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
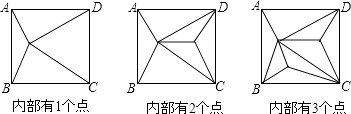 (1)、填写如表:
(1)、填写如表:正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)、如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?(3)、上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.(4)、综上结论,你有什么发现?(写出一条即可)19. 如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度. 20. 甲、乙、丙、丁四人参加某校招聘教师考试,试后甲、乙两人去询问成绩.请你根据下面回答者对甲、乙两人回答的内容进行分析,
20. 甲、乙、丙、丁四人参加某校招聘教师考试,试后甲、乙两人去询问成绩.请你根据下面回答者对甲、乙两人回答的内容进行分析, (1)、列举出这四人的名次排列所有可能出现的不同情况.(2)、求甲排在第一名的概率?21. 已知:如图,正比例函数y=ax的图象与反比例函数y= 的图象交于点A(3,2)
(1)、列举出这四人的名次排列所有可能出现的不同情况.(2)、求甲排在第一名的概率?21. 已知:如图,正比例函数y=ax的图象与反比例函数y= 的图象交于点A(3,2)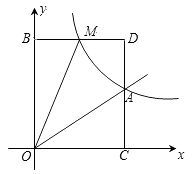 (1)、试确定上述正比例函数和反比例函数的表达式;(2)、根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?(3)、点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.22. 对称轴为直线x=﹣1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(﹣3,0).
(1)、试确定上述正比例函数和反比例函数的表达式;(2)、根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?(3)、点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.22. 对称轴为直线x=﹣1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(﹣3,0).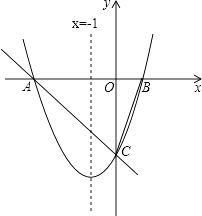 (1)、求点B的坐标.(2)、点C是抛物线与y轴的交点,点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.23. 如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.(1)、如图1,当BC=3时,求DM的长.
(1)、求点B的坐标.(2)、点C是抛物线与y轴的交点,点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.23. 如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.(1)、如图1,当BC=3时,求DM的长. (2)、如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.
(2)、如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.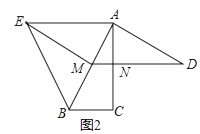
①判断四边形AEMD的形状,并说明理由.
②设BC=x(x>0),四边形AEMD的面积为y,试用含x的式子表示y,并说明是否存在x的值,使得四边形AEMD的面积等于△ABC的面积?若存在,请求出x的值;若不存在,请说明理由.