2017年安徽省江淮十校中考数学二模试卷

试卷更新日期：2017-07-18 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣5的倒数是（）

A、5 B、﹣5 C、 $\frac{1}{5}$ D、﹣ $\frac{1}{5}$

查看试题解析
2. 下列运算中，正确的是（）

A、5a﹣2a=3 B、（x+2y）²=x²+4y² C、x⁸÷x⁴=x² D、（2a）³=8a³

查看试题解析
3. 据统计，中国水资源总量约为27500亿立方米，居世界第六位，其中数据27500亿用科学记数法表示为（）

A、2.75×10⁸ B、2.75×10¹² C、27.5×10¹³ D、0.275×10¹³

查看试题解析
4. 如图，将一个小球摆放在圆柱上底面的正中间，则该几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 立定跳远是小刚同学体育中考的选考项目之一．某次体育课上，体育老师记录了小刚的一组立定跳远训练成绩如下表：
成绩（m）
2.35
2.4
2.45
2.5
2.55
次数
1
1
2
5
1
则下列关于这组数据的说法中正确的是（）

A、众数是2.45 B、平均数是2.45 C、中位数是2.5 D、方差是0.48

查看试题解析
6. 某人沿斜坡坡度i=1：2的斜坡向上前进了6米，则他上升的高度为（）

A、3米 B、 $\frac{6 \sqrt{5}}{5}$ 米 C、2 $\sqrt{3}$ 米 D、 $\frac{12 \sqrt{5}}{5}$ 米

查看试题解析
7. 某广场绿化工程中有一块长2千米，宽1千米的矩形空地，计划在其中修建两块相同的矩形绿地，两块绿地之间既周边留有宽度相等的人行通道（如图），并在这些人行通道铺上瓷砖，要求铺瓷砖的面积是矩形空地面积的 $\frac{1}{2}$ ，设人行通道的宽度为x千米，则下列方程正确的是（）

A、（2﹣3x）（1﹣2x）=1 B、 $\frac{1}{2}$ （2﹣3x）（1﹣2x）=1 C、 $\frac{1}{4}$ （2﹣3x）（1﹣2x）=1 D、 $\frac{1}{4}$ （2﹣3x）（1﹣2x）=2

查看试题解析
8.
如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（　　）

A、AB=AD B、AC=BD C、AD=BC D、AB=CD

查看试题解析
9. 设△ABC的一边长为x，这条边上的高为y，y与x满足的反比例函数关系如图所示．当△ABC为等腰直角三角形时，x+y的值为（）

A、4 B、5 C、5或3 $\sqrt{2}$ D、4或3 $\sqrt{2}$

查看试题解析
10. 已知抛物线y=ax²+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax²+bx+c+2=0无实数根；③a﹣b+c≥0； ④ $\frac{a + b + c}{b - a}$ 的最小值为3．其中正确的是（）

A、①②③ B、②③④ C、①③④ D、①②③④

查看试题解析

二、填空题

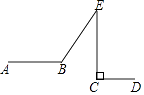
11. 分解因式：ax²﹣6ax+9a= ．

查看试题解析
12. 如图所示，AB∥CD，EC⊥CD．若∠BEC=30°，则∠ABE的度数为．

查看试题解析
13. 如图1，一张纸条上依次写有10个数，如图2，一卡片每次可以盖住纸条上的3个数，那么随机地用卡片盖住的3个数中有且只有一个是负数的概率．

查看试题解析
14. 已知，如图，Rt△ABC中，∠BAC=90°，以AB为直径的⊙O交BC于D，OD交AC的延长线于E，OA=1，AE=3．则下列结论正确的有．
①∠B=∠CAD；②点C是AE的中点；③ $\frac{A D}{B D}$ = $\frac{E D}{A E}$ ；④tan B= $\frac{\sqrt{10} - 1}{3}$ ．

查看试题解析

三、解答题

15. 计算： $\sqrt{12}$ +（﹣ $\frac{1}{2}$ ）^﹣²﹣（ $\sqrt{3}$ ﹣1）⁰﹣2sin60°．

查看试题解析
16. 解方程：x²+4x﹣2=0

查看试题解析
17. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立如图所示的平面直角坐标系．

①将△ABC向左平移7个单位后再向下平移3个单位，请画出两次平移后的△A₁B₁C₁ ，若M为△ABC内的一点，其坐标为（a，b），直接写出两次平移后点M的对应点M₁的坐标；

②以原点O为位似中心，将△ABC缩小，使变换后得到的△A₂B₂C₂与△ABC对应边的比为1：2．请在网格内画出在第三象限内的△A₂B₂C₂ ，并写出点A₂的坐标．

查看试题解析
18. 甲、乙两公司各为“希望工程”捐款2000元．已知乙公司比甲公司人均多捐20元，且乙公司的人数是甲公司人数的 $\frac{4}{5}$ ，问甲、乙两公司人均捐款各多少元？

查看试题解析
19. 如图，AB为⊙O的直径，点C在⊙O上，点P是直径AB上的一点（不与A重合），过点P作AB的垂线交BC于点Q．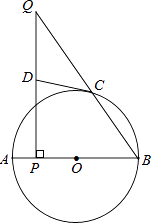

(1)、在线段PQ上取一点D，使DQ=DC，连接DC，试判断CD与⊙O的位置关系，并说明理由．

(2)、若cosB= $\frac{3}{5}$ ，BP=6，AP=1，求QC的长．

查看试题解析
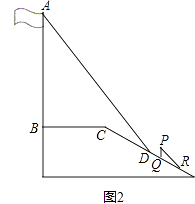
20.
某中学广场上有旗杆如图1所示，在学习解直角三角形以后，数学兴趣小组测量了旗杆的长度．如图2，在某一时刻，光线与水平面的夹角为72°，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为4米，落在斜坡上的影长CD为3米，AB⊥BC，同一时刻，若1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆AB的长度．（结果精确到0.1米．参考数据：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）．

查看试题解析

四、解答题

21. 为加强公路的节水意识，合理利用水资源，某市对居民用水实行阶梯水价，居民家庭每月用水量划分为两个阶梯，一、二阶梯用水的单价之比等于1：2，如图折线表示实行阶梯水价后每月水费y（元）与用水量x（m³）之间的函数关系，其中射线AB表示第二级阶梯时y与x之间的函数关系．

(1)、写出点B的实际意义；

(2)、求射线AB所在直线的表达式．

查看试题解析
22. 若两个二次函数图象的顶点相同，开口大小相同，但开口方向相反，则称这两个二次函数为“对称二次函数”．

(1)、请写出二次函数y=2（x﹣2）²+1的“对称二次函数”；

(2)、已知关于x的二次函数y₁=x²﹣3x+1和y₂=ax²+bx+c，若y₁﹣y₂与y₁互为“对称二次函数”，求函数y₂的表达式，并求出当﹣3≤x≤3时，y₂的最大值．

查看试题解析
23. 如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．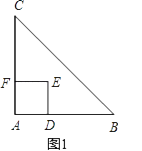

(1)、当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．

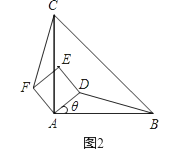(2)、当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．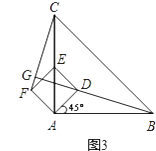
①求证：BD⊥CF；
②当AB=4，AD= $\sqrt{2}$ 时，求线段BG的长．

查看试题解析

成绩（m）	2.35	2.4	2.45	2.5	2.55
次数	1	1	2	5	1