2017年新疆乌鲁木齐市中考数学试卷
试卷更新日期:2017-07-18 类型:中考真卷
一、选择题:
-
1. 如图,数轴上点A表示数a,则|a|是( )
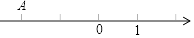 A、2 B、1 C、﹣1 D、﹣22. 如图,直线a∥b,∠1=72°,则∠2的度数是( )
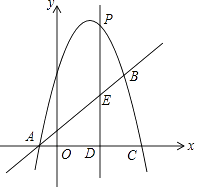
A、2 B、1 C、﹣1 D、﹣22. 如图,直线a∥b,∠1=72°,则∠2的度数是( )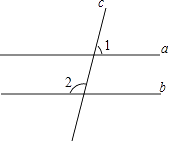 A、118° B、108° C、98° D、72°3. 计算(ab2)3的结果是( )A、3ab2 B、ab6 C、a3b5 D、a3b64. 下列说法正确的是( )A、“经过有交通信号的路口,遇到红灯,”是必然事件 B、已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次 C、处于中间位置的数一定是中位数 D、方差越大数据的波动越大,方差越小数据的波动越小5. 如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )A、4 B、5 C、6 D、76. 一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )
A、118° B、108° C、98° D、72°3. 计算(ab2)3的结果是( )A、3ab2 B、ab6 C、a3b5 D、a3b64. 下列说法正确的是( )A、“经过有交通信号的路口,遇到红灯,”是必然事件 B、已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次 C、处于中间位置的数一定是中位数 D、方差越大数据的波动越大,方差越小数据的波动越小5. 如果n边形每一个内角等于与它相邻外角的2倍,则n的值是( )A、4 B、5 C、6 D、76. 一次函数y=kx+b(k,b是常数,k≠0)的图象,如图所示,则不等式kx+b>0的解集是( )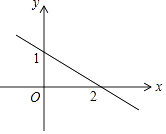 A、x<2 B、x<0 C、x>0 D、x>27. 2017年,在创建文明城市的进程中,乌鲁木齐市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x万棵,可列方程是( )A、﹣ =5 B、﹣ =5 C、+5= D、﹣ =58. 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
A、x<2 B、x<0 C、x>0 D、x>27. 2017年,在创建文明城市的进程中,乌鲁木齐市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x万棵,可列方程是( )A、﹣ =5 B、﹣ =5 C、+5= D、﹣ =58. 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )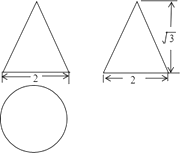 A、π B、2π C、4π D、5π9. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
A、π B、2π C、4π D、5π9. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 且∠AFG=60°,GE=2BG,则折痕EF的长为( )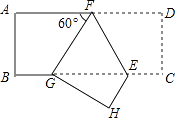 A、1 B、 C、2 D、10.
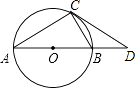
A、1 B、 C、2 D、10.如图,点A(a,3),B(b,1)都在双曲线y= 上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
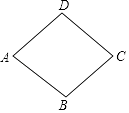
11. 计算|1﹣ |+( )0= .12. 如图,在菱形ABCD中,∠DAB=60°,AB=2,则菱形ABCD的面积为 .
 13. 一件衣服售价为200元,六折销售,仍可获利20%,则这件衣服的进价是元.14. 用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影部分面积为 .
13. 一件衣服售价为200元,六折销售,仍可获利20%,则这件衣服的进价是元.14. 用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影部分面积为 .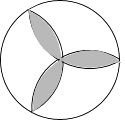 15. 如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论:
15. 如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论:①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .

三、解答题
-
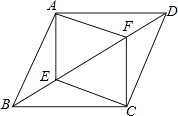
16. 解不等式组: .17. 先化简,再求值:( ﹣ )÷ ,其中x= .18. 我国古代数学名著《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何”,意思是:鸡和兔关在一个笼子里,从上面看有35个头,从下面看有94条腿,问笼中鸡或兔各有多少只?19. 如图,四边形ABCD是平行四边形,E,F是对角线BD上的两点,且BF=ED,求证:AE∥CF.
 20. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
20. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):步数
频数
频率
0≤x<4000
8
a
4000≤x<8000
15
0.3
8000≤x<12000
12
b
12000≤x<16000
c
0.2
16000≤x<20000
3
0.06
20000≤x<24000
d
0.04

请根据以上信息,解答下列问题:
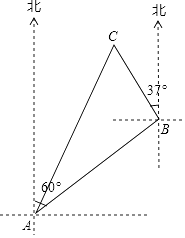
(1)、写出a,b,c,d的值并补全频数分布直方图;(2)、本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?(3)、若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.21.一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ≈1.732,结果取整数)
 22. 一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示:
22. 一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示: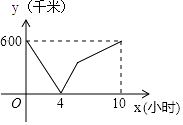 (1)、甲乙两地相距多远?(2)、求快车和慢车的速度分别是多少?(3)、求出两车相遇后y与x之间的函数关系式;(4)、何时两车相距300千米.
(1)、甲乙两地相距多远?(2)、求快车和慢车的速度分别是多少?(3)、求出两车相遇后y与x之间的函数关系式;(4)、何时两车相距300千米.