2017年内蒙古通辽市中考数学试卷
试卷更新日期:2017-07-18 类型:中考真卷
一、选择题
-
1. ﹣5的相反数是( )A、5 B、﹣5 C、 D、2. 下列四个几何体的俯视图中与众不同的是( )A、
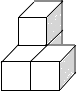 B、
B、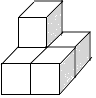 C、
C、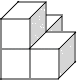 D、
D、 3. 空气是混合物,为直观介绍空气各成分的百分比,最适合用的统计图是( )A、折线图 B、条形图 C、直方图 D、扇形图4. 下列图形中,是轴对称图形,不是中心对称图形的是( )A、
3. 空气是混合物,为直观介绍空气各成分的百分比,最适合用的统计图是( )A、折线图 B、条形图 C、直方图 D、扇形图4. 下列图形中,是轴对称图形,不是中心对称图形的是( )A、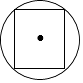 B、
B、 C、
C、 D、
D、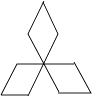 5. 若数据10,9,a,12,9的平均数是10,则这组数据的方差是( )
5. 若数据10,9,a,12,9的平均数是10,则这组数据的方差是( )
A、1 B、1.2 C、0.9 D、1.46. 近似数5.0×102精确到( )A、十分位 B、个位 C、十位 D、百位7. 志远要在报纸上刊登广告,一块10cm×5cm的长方形版面要付广告费180元,他要把该版面的边长都扩大为原来的3倍,在每平方厘米版面广告费相同的情况下,他该付广告费( )A、540元 B、1080元 C、1620元 D、1800元8. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k﹣2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、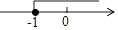 D、
D、 9. 下列命题中,假命题有( )
9. 下列命题中,假命题有( )①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙O的弦AB,CD交于点P,则PA•PB=PC•PD.
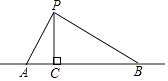
A、4个 B、3个 C、2个 D、1个10.如图,点P在直线AB上方,且∠APB=90°,PC⊥AB于C,若线段AB=6,AC=x,S△PAB=y,则y与x的函数关系图象大致是( )
 A、
A、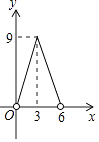 B、
B、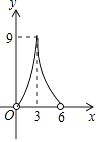 C、
C、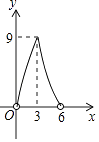 D、
D、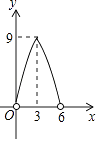
二、填空题
-
11. 2017•通辽)不等式组 的整数解是 .12. 如图,CD平分∠ECB,且CD∥AB,若∠A=36°,则∠B= .
 13. 毛泽东在《沁园春•雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小红将这五位名人简介分别写在五张完全相同的知识卡片上,小哲从中随机抽取一张,卡片上介绍的人物是唐朝以后出生的概率是 .14. 若关于x的二次三项式x2+ax+ 是完全平方式,则a的值是 .15. 在▱ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .16. 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 .
13. 毛泽东在《沁园春•雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小红将这五位名人简介分别写在五张完全相同的知识卡片上,小哲从中随机抽取一张,卡片上介绍的人物是唐朝以后出生的概率是 .14. 若关于x的二次三项式x2+ax+ 是完全平方式,则a的值是 .15. 在▱ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .16. 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 .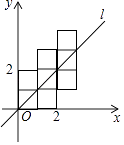 17. 如图,直线y=﹣ x﹣ 与x,y轴分别交于点A,B,与反比例函数y= 的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为 .
17. 如图,直线y=﹣ x﹣ 与x,y轴分别交于点A,B,与反比例函数y= 的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为 .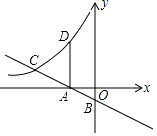
三、解答题
-
18. 计算:(π﹣2017)0+6sin60°﹣|5﹣ |﹣( )﹣2 .19. 先化简,再求值:(1﹣ )÷ ,其中x从0,1,2,3四个数中适当选取.20. 一汽车从甲地出发开往相距240km的乙地,出发后第一小时内按原计划的速度匀速行驶,1小时后比原来的速度加快 ,比原计划提前24min到达乙地,求汽车出发后第1小时内的行驶速度.
21. 2017•通辽)小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.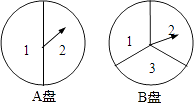 22.
22.如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
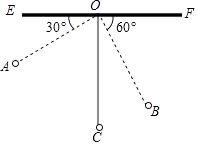 (1)、单摆的长度( ≈1.7);(2)、从点A摆动到点B经过的路径长(π≈3.1).23.
(1)、单摆的长度( ≈1.7);(2)、从点A摆动到点B经过的路径长(π≈3.1).23.某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
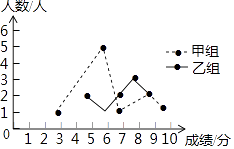 (1)、求出下列成绩统计分析表中a,b的值:
(1)、求出下列成绩统计分析表中a,b的值:组别
平均分
中位数
方差
合格率
优秀率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
(2)、小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.24. 如图,AB为⊙O的直径,D为 的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、连接CD,若OA=AE=4,求四边形ACDE的面积.25.
(1)、求证:DE是⊙O的切线;(2)、连接CD,若OA=AE=4,求四边形ACDE的面积.25.邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
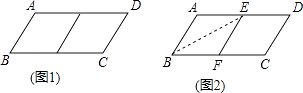 (1)、猜想与计算:
(1)、猜想与计算:邻边长分别为3和5的平行四边形是阶准菱形;已知▱ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出▱ABCD是阶准菱形.
(2)、操作与推理:小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
26.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
 (1)、求抛物线y=ax2+bx+2的函数表达式;(2)、若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;(3)、在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.
(1)、求抛物线y=ax2+bx+2的函数表达式;(2)、若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;(3)、在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.